Question

【题目】已知和外切于，是和的外公切线，，为切点，若，，则到的距离是（ ）

A. B. C. D.

Answer 1

【答案】B

【解析】

先画图，由AB是⊙O1和⊙O2的外公切线，则∠O1AB=∠O2BA=90°，再由O1A=O1M，O2B=O2M，得∠O1AM=∠O1MA，∠O2BM=∠O2MB，则∠BAM+∠AMO1=90°，∠ABM+∠BMO2=90°，则∠AMB=∠BMO2+∠AMO1=90°，再由勾股定理求出AB边上的高．

如图，

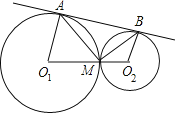
∵AB是⊙O1和⊙O2的外公切线，∴∠O1AB=∠O2BA=90°，
∵O1A=O1M，O2B=O2M，∴∠O1AM=∠O1MA，∠O2BM=∠O2MB，
∴∠BAM+∠AMO1=90°，∠ABM+∠BMO2=90°，
∴∠AMB=∠BMO2+∠AMO1=90°，
∴AM⊥BM，
∵MA=4cm，MB=3cm，
∴由勾股定理得，AB=5cm，

由三角形的面积公式，M到AB的距离是.故选B.