Question

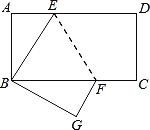
【题目】如图，等边三角形的边长为，点为上的一点，点为上的一点，

连结、，．

求证：①；②；

若，求和的长．

Answer 1

【答案】(1) ①见解析; ②见解析;(2)，．

【解析】

（1）①由△ABC为等边三角形，可得∠B=∠C=60°，又∠APD=60°，由三角形外角的性质可得∠DPC=∠PAB，根据两角对应相等的两个三角形相似即可得△ABP∽△PCD；②利用两角对应相等的两个三角形相似证明△ADP∽△APC，根据相似三角形的性质即可证得结论；（2）由（1）知△ABP∽△PCD，根据相似三角形的性质可得AB：PC=BP：CD，代入数据求得CD的长，即可得AD的长，再利用AP2=ADAC求得AP的长即可．

证明：①在等边三角形中，，
∵，，
∴，
∴；
②∵，，
∴，
∴，
∴；解：∵，，
∴，
∴，
∴，
∵等边三角形的边长为，，，
，，
∴．