题目内容
【题目】如图，在△ABC中，∠ABC和∠ACB的平分线相交于点G，过点G作EF∥BC交AB于E，交AC于F，过点G作GD⊥AC于D，下列四个结论：
①EF＝BE+CF；②∠BGC＝90°+
∠A；③点G到△ABC各边的距离相等；④设GD＝m，AE+AF＝n，则S△AEF＝mn．其中正确的结论有（ ）
A.①②④B.①③④C.①②③D.①②③④
【答案】D
【解析】
根据平行线的性质和角平分线的定义可得∠EBG＝∠EGB，∠FCG＝∠CGF，再根据等角对等边即得BE＝EG，GF＝CF，进而可对①进行判断；
根据角平分线的定义和三角形的内角和即可对②进行判断；
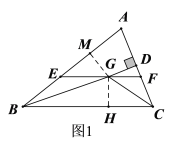
过点G作GM⊥AB于点M，作GH⊥BC于点H，如图1，根据角平分线的性质即可对③进行判断；
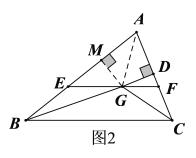
连接AG，如图2，则△AEF的面积=△AEG的面积+△AFG的面积，再根据题意和③的结论即可对④进行判断.
解：①∵∠ABC和∠ACB的平分线相交于点G，
∴∠EBG＝∠CBG，∠BCG＝∠FCG．
∵EF∥BC，
∴∠CBG＝∠EGB，∠BCG＝∠CGF，
∴∠EBG＝∠EGB，∠FCG＝∠CGF，
∴BE＝EG，GF＝CF，
∴EF＝EG+GF＝BE+CF，故本小题正确；
②∵∠ABC和∠ACB的平分线相交于点G，
∴∠GBC+∠GCB＝
（∠ABC+∠ACB）＝（180°﹣∠A），
∴∠BGC＝180°﹣（∠GBC+∠GCB）＝180°﹣（180°﹣∠A）＝90°+∠A，故本小题正确；
③过点G作GM⊥AB于点M，作GH⊥BC于点H，如图1，
∵GB和GC是∠ABC和∠ACB的平分线，
∴GM=GH，GD=GH，
∴GM=GH=GD，
即点G到△ABC各边的距离相等，故本小题正确；
④连接AG，如图2，∵GD＝m，AE+AF＝n，则由③知：GM=GD=m，
∴S△AEF＝AEGM+AFGD＝（AE+AF）m＝nm，故本小题正确．
故选：D．
