题目内容
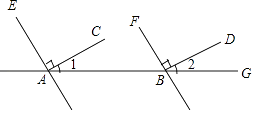
【题目】如图1,已知AB∥CD,∠B=30°,∠D=120°; 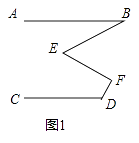
(1)若∠E=60°,则∠F=;
(2)请探索∠E与∠F之间满足的数量关系?说明理由;
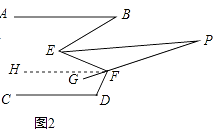
(3)如图2,已知EP平分∠BEF,FG平分∠EFD,反向延长FG交EP于点P,求∠P的度数. 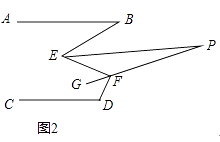
【答案】
(1)90°
(2)解:如图1,分别过点E,F作EM∥AB,FN∥AB,
∴EM∥AB∥FN,
∴∠B=∠BEM=30°,∠MEF=∠EFN,
又∵AB∥CD,AB∥FN,
∴CD∥FN,
∴∠D+∠DFN=180°,
又∵∠D=120°,
∴∠DFN=60°,
∴∠BEF=∠MEF+30°,∠EFD=∠EFN+60°,
∴∠EFD=∠MEF+60°,
∴∠EFD=∠BEF+30°
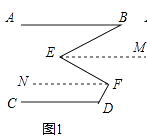
(3)解:如图2,过点F作FH∥EP,
由(2)知,∠EFD=∠BEF+30°,
设∠BEF=2x°,则∠EFD=(2x+30)°,
∵EP平分∠BEF,GF平分∠EFD,
∴∠PEF= ![]() ∠BEF=x°,∠EFG=
∠BEF=x°,∠EFG= ![]() ∠EFD=(x+15)°,
∠EFD=(x+15)°,
∵FH∥EP,
∴∠PEF=∠EFH=x°,∠P=∠HFG,
∵∠HFG=∠EFG﹣∠EFH=15°,
∴∠P=15°
【解析】解:(1)如图1,分别过点E,F作EM∥AB,FN∥AB, ∴EM∥AB∥FN,
∴∠B=∠BEM=30°,∠MEF=∠EFN,
又∵AB∥CD,AB∥FN,
∴CD∥FN,
∴∠D+∠DFN=180°,
又∵∠D=120°,
∴∠DFN=60°,
∴∠BEF=∠MEF+30°,∠EFD=∠EFN+60°,
∴∠EFD=∠MEF+60°
∴∠EFD=∠BEF+30°=90°;
所以答案是:90°;
【考点精析】掌握平行线的性质是解答本题的根本,需要知道两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补.