题目内容
【题目】看图填空,并在括号内注明理由依据, 解:∵∠1=30°,∠2=30°
∴∠1=∠2
∴∥()
又AC⊥AE(已知)
∴∠EAC=90°
∴∠EAB=∠EAC+∠1=120°
同理:∠FBG=∠FBD+∠2=°.
∴∠EAB=∠FBG().
∴∥(同位角相等,两直线平行)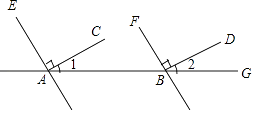
【答案】AC;BD;同位角相等,两直线平行;120;等式的性质;AE;BF
【解析】解:∵∠1=30°,∠2=30°, ∴∠1=∠2.
∴AC∥BD(同位角相等,两直线平行).
又∵AC⊥AE(已知),
∴∠EAC=90°(垂直定义 ),
∴∠EAB=∠EAC+∠1=120°.
同理:∠FBG=∠FBD+∠2=120°.
∴∠EAB=∠FBG(等式的性质).
∴AE∥BF(同位角相等,两直线平行).
所以答案是:AC,BD,同位角相等,两直线平行;120;等式的性质;AE,BF.
【考点精析】通过灵活运用平行线的判定与性质,掌握由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质即可以解答此题.

练习册系列答案
相关题目