Question

【题目】如图，已知EF∥GH，A、D为GH上的两点，M、B为EF上的两点，延长AM于点C，AB平分∠DAC，直线DB平分∠FBC，若∠ACB=100°，则∠DBA的度数为 ．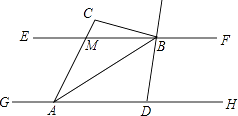

Answer 1

【答案】50°
【解析】解：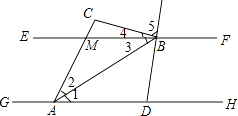
如图，设∠DAB=∠BAC=x，即∠1=∠2=x，
∵EF∥GH，
∴∠2=∠3，
在△ABC内，∠4=180°﹣∠ACB﹣∠1﹣∠3=180°﹣∠ACB﹣2x，
∵直线BD平分∠FBC，
∴∠5= （180°﹣∠4）= （180°﹣180°+∠ACB+2x）= ∠ACB+x，
∴∠DBA=180°﹣∠3﹣∠4﹣∠5
=180°﹣x﹣（180°﹣∠ACB﹣2x）﹣（ ∠ACB+x）
=180°﹣x﹣180°+∠ACB+2x﹣ ∠ACB﹣x
= ∠ACB
= ×100°
=50°．
所以答案是：50°．
【考点精析】通过灵活运用平行线的性质，掌握两直线平行，同位角相等；两直线平行，内错角相等；两直线平行，同旁内角互补即可以解答此题．