题目内容
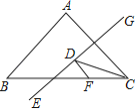
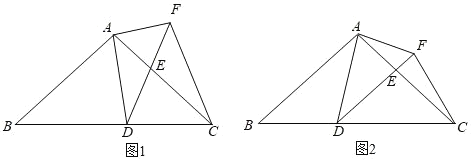
【题目】如图1,在△ABC中,AB=AC=10,BC=16,点D为BC边上的动点(点D不与点B,C重合).以D为顶点作∠ADE=∠B,射线DE交AC边于点E,过点A作AF⊥AD交射线DE于点F,连接CF.
(1)求证:△ABD∽△DCE;
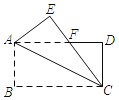
(2)当DE∥AB时(如图2),求AE的长;
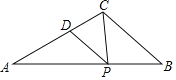
(3)点D在BC边上运动的过程中,是否存在某个位置,使得DF=CF?若存在,求出此时BD的长;若不存在,请说明理由.
【答案】(1)见解析;(2)![]() ;(3)存在,BD=9
;(3)存在,BD=9
【解析】
(1)根据等腰三角形的性质得到![]() ,根据三角形的外角性质得到
,根据三角形的外角性质得到![]() ,根据两角对应相等的两个三角形相似证明即可;
,根据两角对应相等的两个三角形相似证明即可;
(2)证明![]() ,根据相似三角形的性质求出
,根据相似三角形的性质求出![]() ,根据平行线分线段成比例定理列式求出
,根据平行线分线段成比例定理列式求出![]() ;
;
(3)作![]() 于
于![]() ,
,![]() 于
于![]() ,
,![]() 于
于![]() .根据勾股定理求出
.根据勾股定理求出![]() ,证明
,证明![]() ,根据相似三角形的性质求出
,根据相似三角形的性质求出![]() ,根据等腰三角形的性质计算,得到答案.
,根据等腰三角形的性质计算,得到答案.
解:(1)证明:![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,又
,又![]() ,
,
![]() .
.
(2)解:![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() ,即
,即![]() ,
,
解得,![]() ,
,
![]() ,
,
![]()
![]() ,即
,即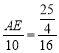 ,
,
解得,![]() ;
;
(3)点![]() 在
在![]() 边上运动的过程中,存在某个位置,使得
边上运动的过程中,存在某个位置,使得![]() .
.
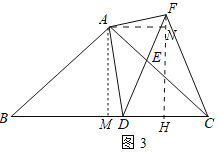
理由如下:如图3,作![]() 于
于![]() ,
,![]() 于
于![]() ,
,![]() 于
于![]() .
.
则四边形![]() 为矩形,
为矩形,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
在![]() 中,由勾股定理,得
中,由勾股定理,得![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() ,即
,即![]() ,
,
解得,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目