题目内容
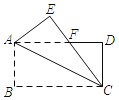
【题目】如图,在矩形ABCD中,AB=4,BC=8,把△ABC沿着AC向上翻折得到△AEC,EC交AD边于点F,则点F到AC的距离是_____.
【答案】![]()
【解析】
由矩形的性质可得AD=BC=8,AD∥BC,AB=CD=4,∠B=∠D=90°,由折叠的性质可得∠ACB=∠FCA,可证AF=CF,由勾股定理可求AF的长,由三角形的面积公式可求点F到AC的距离.
∵四边形ABCD是矩形,
∴AD=BC=8,AD∥BC,AB=CD=4,∠B=∠D=90°,
∴∠FAC=∠ACB,
∵把△ABC沿着AC向上翻折得到△AEC,
∴∠ACB=∠FCA,
∴∠FCA=∠FAC,
∴AF=CF,
∵AB=4,BC=8,
∴AC=![]() ,
,
在Rt△FDC中,CF2=CD2+DF2,
∴AF2=16+(8﹣AF)2,
∴AF=5
∵S△AFC=![]() ×AC×点F到AC的距离=
×AC×点F到AC的距离=![]() ×AF×CD=10
×AF×CD=10
∴点F到AC的距离=![]() ,
,
故答案为:![]()

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目