题目内容
【题目】已知线段AB=3cm,延长线段AB到C,使BC=4cm,延长线段BA到D,使AD=AC,则线段CD的长为________cm.
【答案】14
【解析】
根据线段的和差,可得AC的长,根据线段中点的性质,可得答案.
解:∵AC=AB+BC=3+4=7
∴CD=AD+AC=2AC=14cm
故答案为:14.

练习册系列答案
相关题目
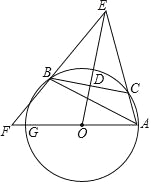
【题目】如图,已知△ABC内接于⊙O,点C在劣弧AB上(不与点A,B重合),点D为弦BC的中点,DE⊥BC,DE与AC的延长线交于点E,射线AO与射线EB交于点F,与⊙O交于点G,设∠GAB=ɑ,∠ACB=β,∠EAG+∠EBA=γ,
(1)点点同学通过画图和测量得到以下近似数据:
ɑ | 30° | 40° | 50° | 60° |
β | 120° | 130° | 140° | 150° |
γ | 150° | 140° | 130° | 120° |
猜想:β关于ɑ的函数表达式,γ关于ɑ的函数表达式,并给出证明:
(2)若γ=135°,CD=3,△ABE的面积为△ABC的面积的4倍,求⊙O半径的长.