题目内容
【题目】已知:如图,在△ABC中,∠ACB=90°,D是BC的中点,DE∥AC,且DE=AC,若AC=2,AD=4,求四边形ACEB的周长.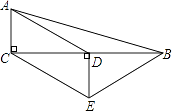
【答案】解:∵DE∥AC,且DE=AC
∴四边形ACED是平行四边形.
∴DE=AC=2.
在Rt△ACD中,由勾股定理得CD= ![]() =2
=2 ![]() .
.
∵D是BC的中点,
∴BC=2CD=4 ![]() .
.
在△ABC中,∠ACB=90°,由勾股定理得AB= ![]() .
.
∵D是BC的中点,DE⊥BC,
∴EB=EC=4.
∴四边形ACEB的周长=AC+CE+EB+BA=10+2 ![]() .
.
【解析】首先判断出四边形ACED是平行四边形.根据平行四边形的性质得出DE=AC=2.在Rt△ACD中,由勾股定理得CD的长,根据中点定义得出BC的长,在△ABC中,∠ACB=90°,由勾股定理得AB的长,根据中垂线定理得出EB=EC=4,根据四边形周长的计算方法得出答案。

练习册系列答案
相关题目