题目内容
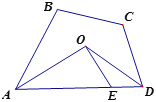
【题目】如图，四边形ABCD中，∠B=104°，∠C=120°，AO、DO分别平分∠BAD和∠CDA，EO⊥AO，则∠EOD＝________
【答案】22°
【解析】
由四边形内角和可求得∠BAD+∠ADC =136°，继而根据角平分线的定义可得∠OAD+∠ODA=68°，再由三角形内角和定理求出∠AOD的度数，由∠AOE=90°，根据∠EOD=∠AOD-∠AOE即可求得答案.
∵四边形ABCD中，∠B=104°，∠C=120°，
∴∠BAD+∠ADC=(4-2)×180°-∠B-∠C=136°，
又AO、DO分别平分∠BAD和∠CDA，
∴∠OAD+∠ODA=
∠BAD+∠ADC=×136°=68°，
∴∠AOD=180°-∠OAD-∠ODA=180°-68°=112°，
又∵EO⊥AO，∴∠AOE=90°，
∴∠EOD=∠AOD-∠AOE=112°-90°=22°，
故答案为：22°.
练习册系列答案
相关题目
