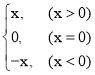题目内容
【题目】已知数轴上有![]() 三点分别表示数
三点分别表示数![]() ,且
,且![]() 满足
满足![]()
![]() .两只电子蚂蚁甲、乙分别从
.两只电子蚂蚁甲、乙分别从![]() 两点同时出发相向而行,若甲的速度为
两点同时出发相向而行,若甲的速度为![]() 个单位/秒,乙的速度为
个单位/秒,乙的速度为![]() 个单位/秒.
个单位/秒.
(1)求![]() 的值并在数轴上标出
的值并在数轴上标出![]() 三点.
三点.

(2)问甲、乙在数轴上的哪个点相遇?
(3)问多少秒后,甲到![]() 的距离为
的距离为![]() 个单位?
个单位?
【答案】(1)![]() ,
,![]() ,
,![]() ;(2)甲、乙在数轴上的点
;(2)甲、乙在数轴上的点![]() 相遇;(3)
相遇;(3)![]() 秒或
秒或![]() 秒后,甲到
秒后,甲到![]() 的距离为
的距离为![]() 个单位.
个单位.
【解析】
(1)根据![]()
![]() 中非负性分别求出a,b,c的值,并标出;
中非负性分别求出a,b,c的值,并标出;
(2)可设x秒后甲与乙相遇,根据甲与乙的路程和为28,可列出方程求解即可;
(3)分为两种情况:甲在B左侧8个单位和甲在B右侧8个单位讨论即可.
解:(1)∵![]()
![]() ,
,
∴a+16=0,b+4=0,c-12=0,
∴A:a=-16,B:b=-4,C:c=12,
在数轴上表示是:

(2)设甲、乙x秒后相遇,
∵数轴上AC相距(16+12)=28个单位,
∴可得:(4+6)x=28,
解得x=2.8,
∴-16+2.8×4=-4.8,
即甲、乙两点在-4.8处相遇;
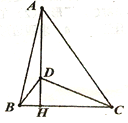
(3)当甲在点B左侧8个单位时,
![]() (秒)
(秒)
当甲在点B右侧8个单位时,
![]() (秒)
(秒)
综上:![]() 秒或
秒或![]() 秒后,甲到
秒后,甲到![]() 的距离为
的距离为![]() 个单位.
个单位.

练习册系列答案
相关题目
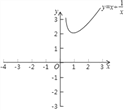
【题目】某数学兴趣小组对函数y=x+![]() 的图象和性质进行了探究,探究过程如下,请补充完整.
的图象和性质进行了探究,探究过程如下,请补充完整.
x | … | ﹣3 | ﹣2 | ﹣1 | - | - |
|
| 1 | 2 | 3 | … |
y | … | - | m | ﹣2 | - | - |
|
| 2 |
|
| … |
(1)自变量x的取值范围是 ,m= .
(2)根据(1)中表内的数据,在如图所示的平面直角坐标系中描点,画出函数图象的一部分,请你画出该函数图象的另一部分.
(3)请你根据函数图象,写出两条该函数的性质;
(4)进一步探究该函数的图象发现:
①方程x+![]() =3有 个实数根;
=3有 个实数根;
②若关于x的方程x+![]() =t有2个实数根,则t的取值范围是 .
=t有2个实数根,则t的取值范围是 .