题目内容
【题目】如图1,已知平行四边形ABCD,BC∥x轴,BC=6,点A的坐标为(1,4),点B的坐标为(﹣3,﹣4),点C在第四象限,点P是平行四边形ABCD边上的一个动点.
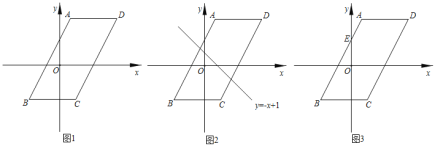
(1)若点P在边CD上,BC=CP,求点P的坐标;
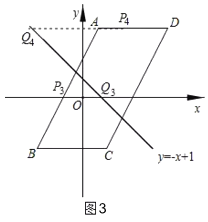
(2)如图2,若点P在边AB,AD上,点P关于坐标轴对称的点Q落在直线y=﹣x+1上,求点P的坐标;
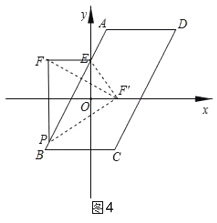
(3)若点P在边AB,AD,BC上,点E是AB与y轴的交点,如图3,过点P作y轴的平行线PF,过点E作x轴的平行线E,它们相交于点F,将△PEF沿直线PE翻折,当点F的对应点落在坐标轴上时,求点P的坐标.(直接写出答案)
【答案】(1)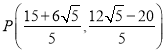 ;(2)P1(﹣3,﹣4),P2(5,4),P3(﹣1,0),P4(3,4);(3)(-
;(2)P1(﹣3,﹣4),P2(5,4),P3(﹣1,0),P4(3,4);(3)(-![]() ,﹣3)或(2,4)或(
,﹣3)或(2,4)或(![]() ,﹣4).
,﹣4).
【解析】
(1)根据平行四边形性质可求得点C、D坐标,再利用待定系数法求直线CD解析式,根据点P在边CD上,BC=CP,可设P(t,2t10),运用两点间距离公式或勾股定理可建立关于t的方程,解方程即可求得P的坐标;
(2)先运用待定系数法求直线AB解析式和直线AD解析式,根据点P关于坐标轴对称的点Q落在直线y=x+1上,分两种情况:①如图2,点P在边AB,AD上,点P关于x轴对称的点Q落在直线y=x+1上,②如图3,点P在边AB,AD上,点P关于y轴对称的点Q落在直线y=x+1上,分别求得点P的坐标即可;
(3)分三种情况:①若点P在边AB上,②若点P在边AD上,③若点P在边BC上,运用翻折性质、勾股定理分别求出点P的坐标.
解:(1)∵平行四边形ABCD
∴AD=BC=6,AB=CD,AB∥CD,AD∥BC
∵BC∥x轴,
∴AD∥x轴,
∵点A的坐标为(1,4),点B的坐标为(﹣3,﹣4),点C在第四象限,
∴C(3,﹣4),D(7,4)
设直线CD解析式为y=kx+b,则![]() ,解得
,解得![]() ,
,
∴直线CD解析式为y=2x﹣10,
∵点P在边CD上,BC=CP,设P(t,2t﹣10),
则(t﹣3)2+[2t﹣10﹣(﹣4)]2=36,
解得:t1=![]() (舍去),t2=
(舍去),t2=![]() ,
,
∴P(![]() ,
,![]() );
);
(2)∵A(1,4),B(﹣3,﹣4),D(7,4)
∴直线AB解析式为y=2x+2,直线AD解析式为y=4,
点P关于坐标轴对称的点Q落在直线y=﹣x+1上,分两种情况:
①如图2,点P在边AB,AD上,点P关于x轴对称的点Q落在直线y=﹣x+1上,
当点P在AB上时,设P(m,2m+2),则Q(m,﹣m+1)
∴2m+2+(﹣m+1)=0,
解得m=﹣3
∴P1(﹣3,﹣4),
当点P在AD上时,设P(m,4),则Q(m,﹣m+1)
∴4﹣m+1=0,
解得:m=5,
∴P2(5,4)
②如图3,点P在边AB,AD上,点P关于y轴对称的点Q落在直线y=﹣x+1上,
当点P在AB上时,设P(m,2m+2),则Q(﹣2m﹣1,2m+2)
∴m﹣2m﹣1=0,
解得:m=﹣1,
∴P3(﹣1,0)
当点P在AD上时,设P(m,4),则Q(﹣3,4),
∴m﹣3=0,
解得:m=3
∴P4(3,4),
综上所述,点P的坐标为:P1(﹣3,﹣4),P2(5,4),P3(﹣1,0),P4(3,4);
(3)在y=2x+2中,令x=0,则y=2,
∴E(0,2),
①若点P在边AB上,如图4设点P(m,2m+2),则F(m,2)
由翻折得:EF′=EF=﹣m,FF′⊥BE
设直线FF′解析式为y=k′x+b′,则k′=![]() ,
,
∴![]() m+b′=2,解得:b′=
m+b′=2,解得:b′=![]() m+2
m+2
∴直线FF′解析式为y=![]() x+
x+![]() m+2,
m+2,
令y=0,得x=m+4,
∴F′(m+4,0),
在Rt△OEF′中,OE2+OF′2=EF′2
∴22+(m+4)2=(﹣m)2,
解得:m=![]() ,
,
∴P(![]() ,﹣3),
,﹣3),
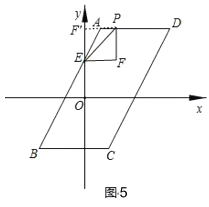
②若点P在边AD上,如图5设P(m,4),则F(m,2),
由题意可知,△PEF沿直线PE翻折后,点F的对应点F′落在y轴上,
由翻折得:EF′=EF=m,∠PEF=∠PEF′
∵EF⊥y轴
∴∠FEF′=90°
∴∠PEF=∠PEF′=45°
∴△PEF是等腰直角三角形
∴EF=PF,即m=2
∴P(2,4),
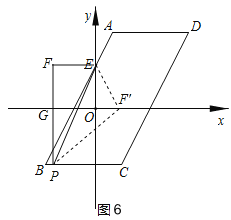
③若点P在边BC上,如图6设PF交x轴于点G,P(m,﹣4),则F(m,2)
∴PF=6,EF=﹣m,PG=4,
由翻折得:EF′=EF=﹣m,PF′=PF=6
∵PF⊥x轴
∴F′G=![]() ,
,
∴F′(m+![]() ,0)
,0)
在Rt△OEF′中,OE2+OF′2=EF′2
∴22+ ( m+![]() )2=m2,
)2=m2,
解得:m=![]() ,
,
∴P(![]() ,﹣4),
,﹣4),
综上所述,点P的坐标为(![]() ,﹣3)或(2,4)或(
,﹣3)或(2,4)或(![]() ,﹣4).
,﹣4).