题目内容
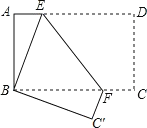
【题目】如图,长方形纸片 ABCD,AD∥BC,将长方形纸片折叠, 使点 D 与点 B 重合,点 C 落在点 C'处,折痕为 EF.
(1)求证:BE=BF.
(2)若∠ABE=18°,求∠BFE 的度数.
(3)若 AB=4,AD=8,求 AE 的长.
【答案】(1)详见解析;(2)57°;(3)3.
【解析】
(1)根据翻折变换的性质,结合矩形的性质证明∠BEF=∠BFE,根据等腰三角形的判定即可得到结论;
(2)根据矩形的性质及等腰三角形的性质即可解决问题;
(3)根据勾股定理列出关于线段 AE 的方程即可解决问题;
解:(1)由题意得:∠BEF=∠DEF;
∵四边形 ABCD 为矩形,
∴DE∥BF,
∴∠BFE=∠DEF,
∴∠BEF=∠BFE,
∴BE=BF;
(2)∵四边形 ABCD 为矩形,
∴∠ABF=90°;而∠ABE=24°,
∴∠EBF=90°-24°=66° ;
又∵BE=BF,
∴∠BFE =![]() =57°;
=57°;
(3)由题意知:BE=DE;
设 E=x,则 BE=DE=8-x,
由勾股定理得:(8-x)2=42+x2,解得:x=3.
即 AE 的长为 3.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目