题目内容
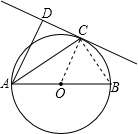
如图，已知AB是⊙O的直径，直线CD与⊙O相切于点C，AC平分∠DAB．
（1）求证：AD⊥DC；
（2）若AD=2，AC=
，求AB的长．
（1）求证：AD⊥DC；
（2）若AD=2，AC=
| 5 |
（1）证明：连接OC
∵直线CD与⊙O相切于点C，
∴OC⊥CD，
∵OA=OC，
∴∠OAC=∠OCA，
∵AC平分∠DAB，
∴∠DAC=∠OAC，
∴∠DAC=∠OCA，
∴OC∥AD，
∴AD⊥CD，
（2）连接BC，则∠ACB=90°，
∵AD⊥CD，
∴∠ADC=∠ACB=90°，
又∵∠DAC=∠OAC，
∴△ADC∽△ACB
∴
=
，
则
=
，
解得：AB=2.5．
∵直线CD与⊙O相切于点C，
∴OC⊥CD，
∵OA=OC，
∴∠OAC=∠OCA，
∵AC平分∠DAB，
∴∠DAC=∠OAC，
∴∠DAC=∠OCA，
∴OC∥AD，
∴AD⊥CD，
（2）连接BC，则∠ACB=90°，
∵AD⊥CD，
∴∠ADC=∠ACB=90°，
又∵∠DAC=∠OAC，
∴△ADC∽△ACB
∴
| AD |
| AC |
| AC |
| AB |
则
| 2 | ||
|
| ||
| AB |
解得：AB=2.5．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
达自己的终点时，另一个点也停止运动，设这两个点从出发运动了t秒．
