Question

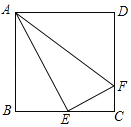
【题目】如图所示，在边长为6的正方形ABCD外以CD为底边作等腰直角△CDE，连接BE，交CD于点F，则CF=___________．

Answer 1

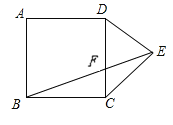
【答案】2

【解析】

作EG⊥BC于G，如图，设DE=CE=a，根据等腰直角三角形的性质得CD= ∠DCE=45°，再利用正方形的性质得CB=CD=，∠BCD=90°，接着判断△CEG为等腰直角三角形得到CG=EG= ，然后在Rt△BEG中根据正切的定义求解，从而可得答案．

解：作EG⊥BC于G，如图，设DE=CE=a，

∵△CDE是以CD为底边的等腰直角三角形，

∴CD= ∠DCE=45°，

∵四边形ABCD为正方形，

∴CB=CD=a，∠BCD=90°，

∴∠ECG=45°，

∴△CEG为等腰直角三角形，

∴CG=EG= ，

在Rt△BEG中，tan∠EBG=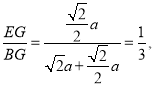

故答案为：