题目内容
【题目】在△ABC中,AB=AC,∠A=60°,点D是线段BC的中点,∠EDF=120°,DE与线段AB相交于点E,DF与线段AC(或AC的延长线)相交于点F.
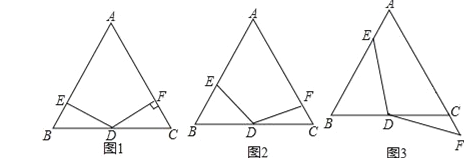
(1)如图1,若DF⊥AC,垂足为F,AB=4,求BE的长;
(2)如图2,将(1)中的∠EDF绕点D顺时针旋转一定的角度,DF仍与线段AC相交于点F.求证:BE+CF=![]() AB.
AB.
(3)如图3,若∠EDF的两边分别交AB、AC的延长线于E、F两点,(2)中的结论还成立吗?如果成立,请证明;如果不成立,请直接写出线段BE、AB、CF之间的数量关系.
【答案】(1)1(2)证明见解析(3)结论不成立.结论:BE﹣CF=![]() AB
AB
【解析】
试题分析:(1)如图1中,只要证明∠BED=90°,根据直角三角形30度角性质即可解决问题.
(2)如图2中,过点D作DM⊥AB于M,作DN⊥AC于N.只要证明△BDM≌△CDN,△EDM≌△FDN即可解决问题.
(3)(2)中的结论不成立.结论:BE﹣CF=![]() AB,证明方法类似(2).
AB,证明方法类似(2).
试题解析:(1)如图1中,
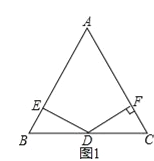
∵AB=AC,∠A=60°,
∴△ABC是等边三角形,
∴∠B=∠C=60°,BC=AC=AB=4,
∵点D是线段BC的中点,
∴BD=DC=![]() BC=2,
BC=2,
∵DF⊥AC,即∠CFD=90°,
∴∠CDF=30°,
又∵∠EDF=120°,
∴∠EDB=30°,
∴∠BED=90°
∴BE=![]() BD=1.
BD=1.
(2)如图2中,过点D作DM⊥AB于M,作DN⊥AC于N.
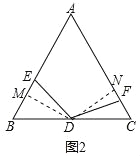
∵∠B=∠C=60°,BD=DC,∠BDM=∠CDN=30°,
∴△BDM≌△CDN,
∴BM=CN,DM=DN,
又∵∠EDF=120°=∠MDN,
∴∠EDM=∠NDF,
又∵∠EMD=∠FND=90°,
∴△EDM≌△FDN,
∴ME=NF,
∴BE+CF=BM+EM+NC﹣FN=2BM=BD=![]() AB.
AB.
(3)结论不成立.结论:BE﹣CF=![]() AB.
AB.
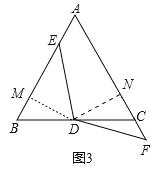
∵∠B=∠C=60°,BD=DC,∠BDM=∠CDN=30°,
∴△BDM≌△CDN,
∴BM=CN,DM=DN,
又∵∠EDF=120°=∠MDN,
∴∠EDM=∠NDF,
又∵∠EMD=∠FND=90°,
∴△EDM≌△FDN,
∴ME=NF,
∴BE﹣CF=BM+EM﹣(FN﹣CN)=2BM=BD=![]() AB.
AB.

 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案