题目内容
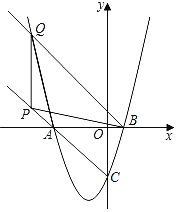
【题目】如图,抛物线y=x2﹣ax+a﹣1与x轴交于A,B两点(点B在正半轴上),与y轴交于点C,OA=3OB.点P在CA的延长线上,点Q在第二象限抛物线上,S△PBQ=S△ABQ.
(1)求抛物线的解析式.
(2)求直线BQ的解析式.
(3)若∠PAQ=∠APB,求点P的坐标.
【答案】(1)y=x2+2x﹣3;(2)y=﹣x+1;(3)点P(﹣4,1).
【解析】
(1)令y=x2﹣ax+a﹣1=0,解得:x=a﹣1或1,故点A、B的坐标分别为:(a﹣1,0)、(1,0),即可求解;
(2)S△PBQ=S△ABQ,则△PBQ和△ABQ底边BQ边上的高相等,故直线PC∥BQ,即可求解;
(3)证明△PBQ≌△AQB(SAS),则∠PQB=∠ABQ=45°,则PQ∥y轴,即可求解.
解:(1)令y=x2﹣ax+a﹣1=0,解得:x=a﹣1或1,
故点A、B的坐标分别为:(a﹣1,0)、(1,0),
∵OA=3OB,故1﹣a=3,解得:a=﹣2,
故抛物线的表达式为:y=x2+2x﹣3;
(2)对于y=x2+2x﹣3,令x=0,则y=﹣3,故点C(0,﹣3),
∵S△PBQ=S△ABQ,
∴△PBQ和△ABQ底边BQ边上的高相等,
故直线PC∥BQ,
设直线AC的表达式为:y=kx+b,则![]() ,解得:
,解得:![]() ,
,
故直线AC的表达式为:y=﹣x﹣3,
则设直线BQ的表达式为:y=﹣x+b,
将点B的坐标代入上式并解得:b=1,
故直线BQ的表达式为:y=﹣x+1;
(3)设直线PB交AQ于点D,

由直线BQ的表达式知∠ABQ=45°,
由(2)知PC∥BQ,
∴∠QAP=∠AQB,∠BPA=∠QBP,
而∠PAQ=∠APB,
∴∠AQB=∠PBQ,
∴DB=DQ,
∵∠PAQ=∠APB,
∴DP=DA,
∴PA=AQ,
而BQ=BQ,
∴△PBQ≌△AQB(SAS),
∴∠PQB=∠ABQ=45°,
∴PQ∥y轴,
联立直线PQ和抛物线的表达式,得 ,解得
,解得![]() 或
或![]() ,
,
即x=1或﹣4(舍去1),
故点Q的横坐标为﹣4,即为点P的横坐标,
而点P在直线AC:y=﹣x﹣3,
故点P(﹣4,1).

 名校课堂系列答案
名校课堂系列答案