题目内容
 如图,平面直角坐标系中有一张透明纸片,透明纸片上有抛物线y=x2及一点P(2,4).若将此透明纸片向右、向上移动后,得抛物线的顶点为(7,2),则此时点P的坐标是
如图,平面直角坐标系中有一张透明纸片,透明纸片上有抛物线y=x2及一点P(2,4).若将此透明纸片向右、向上移动后,得抛物线的顶点为(7,2),则此时点P的坐标是
- A.(9,4)
- B.(9,6)
- C.(10,4)
- D.(10,6)
B
分析:先根据“左加右减、上加下减”的原则得出新抛物线的解析式,再求出P点坐标即可.
解答:∵抛物线y=x2及移动至顶点坐标为(7,2)时的新抛物线解析式为:y=(x-7)2+2,即先向右平移7个单位,再向上平移2个单位,
∴P(2,4)应先向右平移7个单位,再向上平移2个单位,其新坐标变为(2+7,4+2),
即(9,6).
故选B.
点评:本题考查的是二次函数的图象与几何变换,能根据题意得出新抛物线的解析式是解答此题的关键.
分析:先根据“左加右减、上加下减”的原则得出新抛物线的解析式,再求出P点坐标即可.
解答:∵抛物线y=x2及移动至顶点坐标为(7,2)时的新抛物线解析式为:y=(x-7)2+2,即先向右平移7个单位,再向上平移2个单位,
∴P(2,4)应先向右平移7个单位,再向上平移2个单位,其新坐标变为(2+7,4+2),
即(9,6).
故选B.
点评:本题考查的是二次函数的图象与几何变换,能根据题意得出新抛物线的解析式是解答此题的关键.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
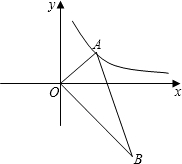 如图,平面直角坐标系中,O为直角三角形ABC的直角顶点,∠B=30°,锐角顶点A在双曲线
如图,平面直角坐标系中,O为直角三角形ABC的直角顶点,∠B=30°,锐角顶点A在双曲线 =2
=2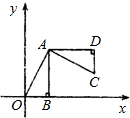 如图,平面直角坐标系中,OB在x轴上,∠ABO=90°,点A的坐标为(1,2).将△AOB绕点A逆时针旋转90°,则点O的对应点C的坐标为( )
如图,平面直角坐标系中,OB在x轴上,∠ABO=90°,点A的坐标为(1,2).将△AOB绕点A逆时针旋转90°,则点O的对应点C的坐标为( )
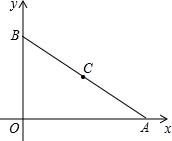 如图在平面直角坐标系中,A点坐标为(8,0),B点坐标为(0,6)C是线段AB的中点.请问在y轴上是否存在一点P,使得以P、B、C为顶点的三角形与△AOB相似?若存在,求出P点坐标;若不存在,说明理由.
如图在平面直角坐标系中,A点坐标为(8,0),B点坐标为(0,6)C是线段AB的中点.请问在y轴上是否存在一点P,使得以P、B、C为顶点的三角形与△AOB相似?若存在,求出P点坐标;若不存在,说明理由.