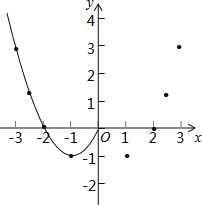题目内容
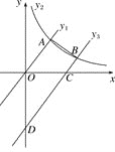
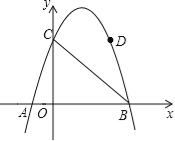
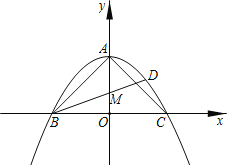
【题目】如图,等腰直角△ABC,OC=2,抛物线y=ax2+c过A,B,C三点,D为抛物线上一点,连接BD且tan∠DBC=![]() .
.

(1)求直线BD和抛物线所表示的函数解析式.
(2)如果在抛物线上有一点E,使得S△EBC=S△ABD,求这时E点坐标.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() 或
或 或
或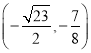
【解析】
(1)根据题意得到A(0,2),B(2,0),C(2,0),根据待定系数法即可求得抛物线的解析式,设BD与y轴的交点为M,由tan∠DBC=![]() ,求得M的坐标为(0,1),根据待定系数法即可求得直线BD的解析式;
,求得M的坐标为(0,1),根据待定系数法即可求得直线BD的解析式;
(2)解析式联立求得D的坐标,然后根据S△ABD=S△ABM+S△ADM求得△EBC面积,根据面积公式求得E的纵坐标,把纵坐标代入抛物线解析式即可求得横坐标,得到E的坐标.
(1)等腰直角△ABC,OC=2,
∴OA=OB=OC=2,
∴A(0,2),B(﹣2,0),C(2,0),
∵抛物线y=ax2+c过A,B,C三点,
∴![]() ,解得
,解得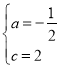 ,
,
∴抛物线的解析式为y=﹣![]() +2;
+2;
∵tan∠DBC=![]() ,
,
设BD与y轴的交点为M,
∴![]() =
=![]() ,
,
∴OM=2×![]() =1,
=1,
∴M(0,1),
设直线BD的解析式为y=kx+b,
把B(﹣2,0),M(0,1)代入得![]() ,
,
解得![]() ,
,
∴直线BD的解析式为y=![]() +1;
+1;
(2)解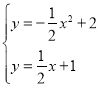 得
得![]() 或
或![]() ,
,
∴D(1,![]() ),
),
∴S△ABD=S△ABM+S△ADM=![]() ×(2﹣1)×2+
×(2﹣1)×2+![]() (2﹣1)×
(2﹣1)×![]() =
=![]() ,
,
∵S△EBC=S△ABD,
∴![]() BC|yE|=
BC|yE|=![]() ,即
,即![]() |yE|=
|yE|=![]() ,
,
∴|yE|=![]() ,
,
∴E的纵坐标为±![]() ,
,
把y=![]() 代入y=﹣
代入y=﹣![]() +2得,
+2得,![]() =﹣
=﹣![]() +2,
+2,
解得x=±![]() ,
,
把y=﹣![]() 代入y=﹣
代入y=﹣![]() +2得,﹣
+2得,﹣![]() =﹣
=﹣![]() +2,
+2,
解得x=±![]() ,
,
∴E点的坐标为(![]() ,
,![]() )或(﹣
)或(﹣![]() ,
,![]() )或(
)或(![]() ,﹣
,﹣![]() )或(﹣
)或(﹣![]() ,﹣
,﹣![]() ).
).

 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案【题目】某班“数学兴趣小组”对函数y=x2﹣2|x|的图象和性质进行了探究,探究过程如下,请补充完整:
(1)自变量x的取值范围是全体实数,x与y的几组对应值列表如下:
x | … | ﹣3 |
| ﹣2 | ﹣1 | 0 | 1 | 2 |
| 3 | … |
y | … | 3 |
| m | ﹣1 | 0 | ﹣1 | 0 |
| 3 | … |
其中,m= .
(2)根据表中数据,在如图所示的平面直角坐标系中描点,并画出了函数图象的一部分,请画出该函数图象的另一部分.
(3)探究函数图象发现:
①函数图象与x轴有 个交点,所以对应的方程x2﹣2|x|=0有 个实数根;
②方程x2﹣2|x|=![]() 有 个实数根;
有 个实数根;
③关于x的方程x2﹣2|x|=a有4个实数根时,a的取值范围是 .