��Ŀ����
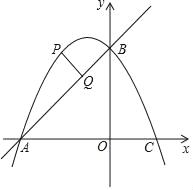
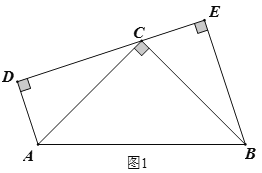
����Ŀ����ͼ��ֱ��y1��![]() x��˫����y2��
x��˫����y2��![]() (x��0)���ڵ�A����ֱ��y1��
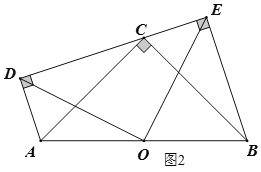
(x��0)���ڵ�A����ֱ��y1��![]() x����ƽ��4����λ��Ƹ�ֱ��Ϊy3����y3��˫���߽���B����x�ύ��C����y�ύ��D��AO��2BC������AB�������½��۴������(����)
x����ƽ��4����λ��Ƹ�ֱ��Ϊy3����y3��˫���߽���B����x�ύ��C����y�ύ��D��AO��2BC������AB�������½��۴������(����)
����C����Ϊ(3,0)����k��![]() ����S�ı���OCBA��
����S�ı���OCBA��![]() ������2��x��4ʱ����y1��y2��y3����S�ı���ABDO��2S��COD.
������2��x��4ʱ����y1��y2��y3����S�ı���ABDO��2S��COD.
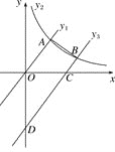
A. 1�� B. 2�� C. 3�� D. 4��
���𰸡�A
��������
����һ�κ���ͼ���ƽ�ƹ��ɣ���y1=![]() x����ƽ��4����λ�õ�ֱ��BC�Ľ���ʽΪy3=
x����ƽ��4����λ�õ�ֱ��BC�Ľ���ʽΪy3=![]() x-4��Ȼ���y=0����ȷ��C�����꣬�����жϢ٣���AE��x����E�㣬BF��x����F�㣬��֤��Rt��OAE�ס�RtCBF����
x-4��Ȼ���y=0����ȷ��C�����꣬�����жϢ٣���AE��x����E�㣬BF��x����F�㣬��֤��Rt��OAE�ס�RtCBF����![]() =
=![]() =
=![]() =2������A��������a��
=2������A��������a��![]() a������CF=
a������CF=![]() a��BF=
a��BF=![]() a���õ�B�����꣨3+
a���õ�B�����꣨3+![]() a��
a��![]() a����Ȼ����ݷ����������ϵ������������a
a����Ȼ����ݷ����������ϵ������������a![]() a=��3+
a=��3+![]() a��
a��![]() a�����a=2�����ǿ�ȷ����A������Ϊ��2��
a�����a=2�����ǿ�ȷ����A������Ϊ��2��![]() �����ٽ�A���������y2=
�����ٽ�A���������y2=![]() �����k��ֵ�������жϢڣ�����S�ı���OCBA=S��OAE+S����AEFB-S��BCF�����S�ı���OCBA�������жϢۣ�����ͼ��ó���2��x��4ʱ��ֱ��y1��˫����y2���Ϸ���˫����y2����ֱ��y3���Ϸ��������жϢܣ��ȸ��������������ʽ���S��COD=
�����k��ֵ�������жϢڣ�����S�ı���OCBA=S��OAE+S����AEFB-S��BCF�����S�ı���OCBA�������жϢۣ�����ͼ��ó���2��x��4ʱ��ֱ��y1��˫����y2���Ϸ���˫����y2����ֱ��y3���Ϸ��������жϢܣ��ȸ��������������ʽ���S��COD=![]() ��3��4=6������S�ı���ABDO=S�ı���OCBA+S��OCD���ó�S�ı���ABDO=12�������жϢݣ�
��3��4=6������S�ı���ABDO=S�ı���OCBA+S��OCD���ó�S�ı���ABDO=12�������жϢݣ�
�⣺�١߽�ֱ��y1��![]() x����ƽ��4����λ��Ƹ�ֱ��Ϊy3��y3��˫���߽���B����x�ύ��C��
x����ƽ��4����λ��Ƹ�ֱ��Ϊy3��y3��˫���߽���B����x�ύ��C��
��ֱ��BC�Ľ���ʽΪy3��![]() x��4��
x��4��
��y��0���룬��![]() x��4��0�����x��3��
x��4��0�����x��3��
��C������Ϊ(3,0)���ʱ�������ȷ��
����AE��x����E�㣬
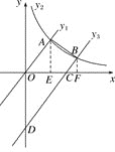
��OA��BC��
���AOC����BCF��
��Rt��OAE��Rt��CBF��
��![]() ��
��![]() ��
��![]() ��2��
��2��
��A������Ϊ![]() ����OE��a��AE��
����OE��a��AE��![]() a��
a��
��CF��![]() a��BF��
a��BF��![]() a��
a��
��OF��OC��CF��3��![]() a��
a��
��B������Ϊ![]() ��
��
�ߵ�A���B����y2��![]() (x��0)��ͼ���ϣ�
(x��0)��ͼ���ϣ�
��a��![]() a��
a��![]() ��
��![]() a�����a��2��
a�����a��2��
���A������Ϊ![]() ��
��
��A![]() ����y��
����y��![]() ��
��
��k��2��![]() ��
��![]() ���ʱ�������ȷ��
���ʱ�������ȷ��
�ۡ�A![]() ��B
��B![]() ��CF��
��CF��![]() a��1��
a��1��
��S�ı���OCBA��S��OAE��S����AEFB��S��BCF
��![]() ��2��
��2��![]() ��
��![]() ��
��![]() ��2��
��2��![]() ��1��
��1��![]()
��![]() ��4��
��4��![]()
��6���ʱ����۴���
����ͼ���֪����2��x��4ʱ����y1��y2��y3���ʱ�������ȷ��
�ݡ�S��COD��![]() ��3��4��6��S�ı���ABDO��S�ı���OCBA��S��OCD��6��6��12��
��3��4��6��S�ı���ABDO��S�ı���OCBA��S��OCD��6��6��12��
��S�ı���ABDO��2S��COD���ʱ�������ȷ��
��ѡA.

����Ŀ��ij��ѧ����С����������ѹǿʵ��ʱ�����ѹǿp(Pa)�����V(cm3)֮�������ж�Ӧ���ݣ�
p(Pa) | �� | 1 | 2 | 3 | 4 | 5 | �� |
V(cm3) | �� | 6 | 3 | 2 | 1.5 | 1.2 | �� |
���ݱ����ṩ����Ϣ���ش��������⣺
(1)����p��V֮��Ĺ�ϵ�������������ϵʽ��
(2)������������12cm3ʱ��ѹǿ�Ƕ��٣�