题目内容
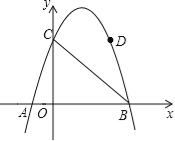
【题目】如图,抛物线y=﹣x2+3x+4与x轴交于A、B两点,与y轴交于C点,点D在抛物线上且横坐标为3.
(1)求tan∠DBC的值;
(2)点P为抛物线上一点,且∠DBP=45°,求点P的坐标.
【答案】(1)tan∠DBC=![]() ;
;
(2)P(﹣![]() ,
,![]() ).
).
【解析】
(1)连接CD,过点D作DE⊥BC于点E.利用抛物线解析式可以求得点A、B、C、D的坐标,则可得CD//AB,OB=OC,所以∠BCO=∠BCD=∠ABC=45°.由直角三角形的性质、勾股定理和图中相关线段间的关系可得BC=4![]() ,BE=BC﹣DE=
,BE=BC﹣DE=![]() .由此可知tan∠DBC=
.由此可知tan∠DBC=![]() ;
;
(2)过点P作PF⊥x轴于点F.由∠DBP=45°及∠ABC=45°可得∠PBF=∠DBC,利用(1)中的结果得到:tan∠PBF=![]() .设P(x,﹣x2+3x+4),则利用锐角三角函数定义推知
.设P(x,﹣x2+3x+4),则利用锐角三角函数定义推知![]()
![]() ,通过解方程求得点P的坐标为(﹣
,通过解方程求得点P的坐标为(﹣![]() ,
,![]() ).
).
(1)令y=0,则﹣x2+3x+4=﹣(x+1)(x﹣4)=0,
解得 x1=﹣1,x2=4.
∴A(﹣1,0),B(4,0).
当x=3时,y=﹣32+3×3+4=4,
∴D(3,4).
如图,连接CD,过点D作DE⊥BC于点E.

∵C(0,4),
∴CD//AB,
∴∠BCD=∠ABC=45°.
在直角△OBC中,∵OC=OB=4,
∴BC=4![]() .
.
在直角△CDE中,CD=3.
∴CE=ED=![]() ,
,
∴BE=BC﹣DE=![]() .
.
∴tan∠DBC=![]() ;
;
(2)过点P作PF⊥x轴于点F.
∵∠CBF=∠DBP=45°,
∴∠PBF=∠DBC,
∴tan∠PBF=![]() .
.
设P(x,﹣x2+3x+4),则![]() ,
,
解得 x1=﹣![]() ,x2=4(舍去),
,x2=4(舍去),
∴P(﹣![]() ,
,![]() )..
)..

 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案【题目】近代统计学的发展起源于二十世纪初,它是在概率论的基础上发展起来的,但统计性质的工作可以追溯到远古的“结绳记事”和《二十四史》中大量的关于我国人口、钱粮、水文、天文、地震等资料的记录.现代数理统计的奠基人是英国数学家和生物学家费希尔,毕业于剑桥大学,长期在农业试验站做生物实验.费尔希在高等植物基因性状研究实验中,从若干紫花与白花中各随机抽取20株测量高度(植株正常高度![]() 的取值范围为
的取值范围为![]() ),过程如下:
),过程如下:
收集数据(单位:![]() ):
):
紫花:42,42,28,54,29,52,44,36,39,49,33,40,35,52,29,32,51,55,42,38
白花植株高度为![]() 的数据有:35,37,37,38,39,40,42,42
的数据有:35,37,37,38,39,40,42,42
整理数据:
数据分为六组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
组别 |
|
|
|
|
|
|
紫花数量 | 3 | 2 |
| 5 | 1 | 5 |

分析数据:
植株 | 平均数 | 众数 | 中位数 | 方差 |
紫花 | 41.1 | 42 | 41 | 8.8 |
白花 | 40.25 | 43 |
| 7.2 |
应用数据:
(1)请写出表中![]() ,
,![]() ;
;
(2)估计500株紫花中高度正常的有多少株?
(3)结合上述数据信息,请判断哪种花长势更均匀,并说明理由(一条理由即可).