Question

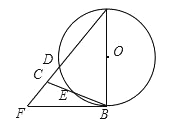
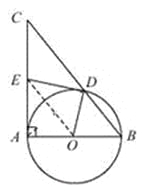
【题目】如图，在△ABC中，∠CAB＝90°，∠CBA＝50°，以AB为直径作⊙O交BC于点D，点E在边AC上，且满足ED＝EA．

（1）求∠DOA的度数；

（2）求证：直线ED与⊙O相切．

Answer 1

【答案】（1）∠DOA =100°；（2）证明见解析.

【解析】

试题（1）根据∠CBA=50°，利用圆周角定理即可求得∠DOA的度数；（2）连接OE，利用SSS证明△EAO≌△EDO，根据全等三角形的性质可得∠EDO=∠EAO=90°，即可证明直线ED与⊙O相切．

试题解析：（1）∵∠DBA=50°，∴∠DOA=2∠DBA=100°；

（2）证明：连接OE，

在△EAO和△EDO中，

AO=DO，EA=ED，EO=EO，

∴△EAO≌△EDO，

得到∠EDO=∠EAO=90°，

∴直线ED与⊙O相切．