题目内容
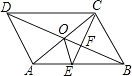
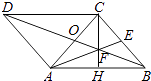
【题目】如图,在ABCD中,AC为对角线,AC=BC=5,AB=6,AE是△ABC的中线.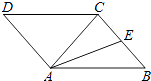
(1)用无刻度的直尺画出△ABC的高CH(保留画图痕迹);
(2)求△ACE的面积.
【答案】
(1)解:如图,连接BD,BD与AE交于点F,连接CF并延长到AB,则它与AB的交点即为H.
理由如下:
∵BD、AC是ABCD的对角线,
∴点O是AC的中点,
∵AE、BO是等腰△ABC两腰上的中线,
∴AE=BO,AO=BE,
∵AO=BE,
∴△ABO≌△BAE(SSS),
∴∠ABO=∠BAE,
△ABF中,∵∠FAB=∠FBA,∴FA=FB,
∵∠BAC=∠ABC,
∴∠EAC=∠OBC,
由 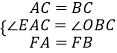 可得△AFC≌BFC(SAS)
可得△AFC≌BFC(SAS)
∴∠ACF=∠BCF,即CH是等腰△ABC顶角平分线,
所以CH是△ABC的高;
(2)解:∵AC=BC=5,AB=6,CH⊥AB,
∴AH= ![]() AB=3,
AB=3,
∴CH= ![]() =4,
=4,
∴S△ABC= ![]() ABCH=
ABCH= ![]() ×6×4=12,
×6×4=12,
∵AE是△ABC的中线,
∴S△ACE= ![]() S△ABC=6.
S△ABC=6.
【解析】此题考查了平行四边形的性质、等腰三角形的性质、勾股定理以及三角形中线的性质.注意三角形的中线把三角形分成面积相等的两部分.(1)连接BD,BD与AE交于点F,连接CF并延长到AB,与AB交于点H,则CH为△ABC的高;(2)首先由三线合一,求得AH的长,再由勾股定理求得CH的长,继而求得△ABC的面积,又由AE是△ABC的中线,求得△ACE的面积.
【考点精析】根据题目的已知条件,利用平行四边形的性质的相关知识可以得到问题的答案,需要掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分.

练习册系列答案
相关题目