题目内容
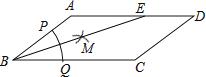
【题目】如图,在△ABC的一边AB上有一点P.
(1)能否在另外两边AC和BC上各找一点M、N,使得△PMN的周长最短.若能,请画出点M、N的位置,若不能,请说明理由;
(2)若∠ACB=40°,在(1)的条件下,求出∠MPN的度数.

【答案】(1)详见解析.(2)100°.
【解析】
(1)如图:作出点P关于AC、BC的对称点D、G,然后连接DG交AC、BC于两点,标注字母M、N;
(2)根据对称的性质,易求得∠C+∠EPF=180°,由∠ACB=48°,易求得∠D+∠G=48°,即而求得答案.
解:(1)①作出点P关于AC、BC的对称点D、G,
②连接DG交AC、BC于两点,
③标注字母M、N;

(2)∵PD⊥AC,PG⊥BC,
∴∠PEC=∠PFC=90°,
∴∠C+∠EPF=180°,
∵∠C=40°,
∴∠EPF=140°,
∵∠D+∠G+∠EPF=180°,
∴∠D+∠G=40°,
由对称可知:∠G=∠GPN,∠D=∠DPM,
∴∠GPN+∠DPM=40°,
∴∠MPN=140°-40°=100°.

练习册系列答案
相关题目
【题目】某校在践行“社会主义核心价值观”演讲比赛中,对名列前20名的选手的综合分数m进行分组统计,结果如表所示:
组号 | 分组 | 频数 |
一 | 6≤m<7 | 2 |
二 | 7≤m<8 | 7 |
三 | 8≤m<9 | a |
四 | 9≤m≤10 | 2 |

(1)求a的值;
(2)若用扇形图来描述,求分数在8≤m<9内所对应的扇形图的圆心角大小;
(3)将在第一组内的两名选手记为:A1、A2 , 在第四组内的两名选手记为:B1、B2 , 从第一组和第四组中随机选取2名选手进行调研座谈,求第一组至少有1名选手被选中的概率(用树状图或列表法列出所有可能结果).