题目内容
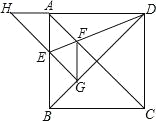
【题目】在⊙O中，弧AB所对的圆心角∠AOB＝108°，点C为⊙O上的动点，以AO、AC为边构造AODC．当∠A＝_____°时，线段BD最长．
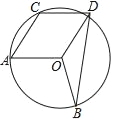
【答案】27°
【解析】
如图，连接OC，延长OA交⊙O于F，连接DF．由△DOF≌△CAO，可得DF=OC，推出点D的运动轨迹是F为圆心OC为半径的圆，推出当点D在BF的延长线上时，BD的值最大，由此即可解决问题.
如图，连接OC，延长OA交⊙O于F，连接DF．
∵四边形ACDO是平行四边形，
∴∠DOF=∠A，DO=AC，
∵OF=AO，
∴△DOF≌△CAO，
∴DF=OC，
∴点D的运动轨迹是F为圆心OC为半径的圆，
∴当点D在BF的延长线上时，BD的值最大，
∵∠AOB=108°，
∴∠FOB=72°，
∵OF=OB，
∴∠OFB=54°，
∵FD=FO，
∴∠FOD=∠FDO=27°，
∴∠A=∠FOD=27°.
故答案为27°.
练习册系列答案
阅读快车系列答案
相关题目
