题目内容
(1)计算:|-12|+50-
-sin45°-2tan60°+(cos30°)-1
(2)先化简,再求值:1-
÷
,其中a=
,b=1.
(3)解不等式组:
,并把其解集在数轴上表示出来.
| 2 |
(2)先化简,再求值:1-
| a-b |
| a+2b |
| a2-b2 |
| a2+4ab+4b2 |
| 2 |
(3)解不等式组:
|
分析:(1)分别根据绝对值的性质以及特殊角的三角函数值、负指数幂的性质、零指数幂的性质进行化简得出即可;
(2)先根据分式混合运算的法则把原式进行化简,再把a,b的值代入进行计算即可;
(3)分别解出两个不等式组,进而结合数轴得出不等式解集即可.
(2)先根据分式混合运算的法则把原式进行化简,再把a,b的值代入进行计算即可;
(3)分别解出两个不等式组,进而结合数轴得出不等式解集即可.
解答:解:(1)
|-12|+50-
-sin45°-2tan60°+(cos30°)-1
=12+1-
-
-2
+
=13-
-
;
(2)1-
÷
,
=1-
×
=1-
=
,
把a=
,b=1代入原式得:
原式=
=
=1-
;
(3)
,
解①得:x≤3,
解②得:x>-2,
故不等式组的解集为:-2<x≤3,
在数轴上表示为:
 .
.
|-12|+50-
| 2 |
=12+1-
| 2 |
| ||
| 2 |
| 3 |
| 1 | ||||
|
=13-
3
| ||
| 2 |
4
| ||
| 3 |
(2)1-
| a-b |
| a+2b |
| a2-b2 |
| a2+4ab+4b2 |
=1-
| a-b |
| a+2b |
| (a+2b)2 |
| (a+b)(a-b) |
=1-
| a+2b |
| a+b |
=
| -b |
| a+b |
把a=
| 2 |
原式=
| -b |
| a+b |
| -1 | ||
|
| 2 |
(3)
|
解①得:x≤3,
解②得:x>-2,
故不等式组的解集为:-2<x≤3,
在数轴上表示为:
 .
.点评:本题考查的是分式的化简求值以及实数的运算和不等式组的解法等知识,在解答此类题目时要注意通分及约分的灵活应用.

练习册系列答案
相关题目
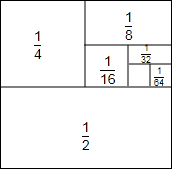 如图所示,把一个面积为1的正方形等分成两个面积为
如图所示,把一个面积为1的正方形等分成两个面积为