题目内容
 如图所示,把一个面积为1的正方形等分成两个面积为
如图所示,把一个面积为1的正方形等分成两个面积为| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 8 |
(1)第7次等分所得的一个长方形面积是多少?
(2)试利用图形揭示的规律计算:
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 16 |
| 1 |
| 32 |
| 1 |
| 64 |
| 1 |
| 128 |
分析:(1)根据题意得到第1次等分所得的一个长方形面积=(
)1,第2次等分所得的一个长方形面积=
=(
)2,第2次等分所得的一个长方形面积=
=(
)3,则
第n次等分所得的一个长方形面积=(
)n,然后把n=7代入计算即可;
(2)根据图形揭示的规律,把一个面积为1的正方形分7次得到的面积为
+
+
+
+
+
+…+
+
,则
+
+
+
+
+
+…+
=1-
,然后通分计算即可.
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 8 |
| 1 |
| 2 |
第n次等分所得的一个长方形面积=(
| 1 |
| 2 |
(2)根据图形揭示的规律,把一个面积为1的正方形分7次得到的面积为
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 16 |
| 1 |
| 32 |
| 1 |
| 64 |
| 1 |
| 128 |
| 1 |
| 128 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 16 |
| 1 |
| 32 |
| 1 |
| 64 |
| 1 |
| 128 |
| 1 |
| 128 |
解答:解:∵第1次等分所得的一个长方形面积=(
)1,
第2次等分所得的一个长方形面积=
=(
)2,
第2次等分所得的一个长方形面积=
=(
)3,
∴第7次等分所得的一个长方形面积=(
)7=
;
(2)
+
+
+
+
+
+…+
=1-
=
.
| 1 |
| 2 |
第2次等分所得的一个长方形面积=
| 1 |
| 4 |
| 1 |
| 2 |
第2次等分所得的一个长方形面积=
| 1 |
| 8 |
| 1 |
| 2 |
∴第7次等分所得的一个长方形面积=(
| 1 |
| 2 |
| 1 |
| 128 |
(2)
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 16 |
| 1 |
| 32 |
| 1 |
| 64 |
| 1 |
| 128 |
=1-
| 1 |
| 128 |
=
| 127 |
| 128 |
点评:本题考查了规律型:数字的变化类:认真观察、仔细思考,善用联想是解决这类问题的方法.

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
 与CB的延长线上的点E重合.
与CB的延长线上的点E重合. 的矩形,接着把面积为
的矩形,接着把面积为 的矩形等分成面积为
的矩形等分成面积为 的正方形,再把面积为
的正方形,再把面积为 的正方形等分成面积为了
的正方形等分成面积为了 的矩形,如此下去,试用图形揭示规律计算:
的矩形,如此下去,试用图形揭示规律计算: .
.
 的矩形,接着把面积为
的矩形,接着把面积为 的矩形等分成面积为
的矩形等分成面积为 的正方形,再把面积为
的正方形,再把面积为 的正方形等分成面积为
的正方形等分成面积为 的矩形,如此下去,试用图形揭示规律计算:
的矩形,如此下去,试用图形揭示规律计算: .
.
 如图所示,把一个面积为1的正方形等分成两个面积为
如图所示,把一个面积为1的正方形等分成两个面积为 的长方形,接着再把面积为
的长方形,接着再把面积为 的长方形,再把面积为
的长方形,再把面积为 的长方形,如此进行下去.
的长方形,如此进行下去.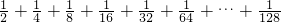 .
.