ЬтФПФкШн
ЁОЬтФПЁПЖдгкЦНУцжБНЧзјБъЯЕxOyжаЕФЕуPЃЈaЃЌbЃЉЃЌШєЕуP1ЕФзјБъЮЊЃЈa+kbЃЌka+bЃЉЃЈЦфжаkЮЊГЃЪ§ЃЌЧвkЁй0ЃЉЃЌдђГЦЕуP1ЮЊЕуPЕФЁАkЪєХЩЩњЕуЁБЃЎ
Р§ШчЃЌPЃЈ1ЃЌ4ЃЉЕФЁА2ЪєХЩЩњЕуЁБЮЊP1ЃЈ1+2ЁС4ЃЌ2ЁС1+4ЃЉЃЌМДP1ЃЈ9ЃЌ6ЃЉЃЎ
ЃЈ1ЃЉЕуЃЈЉ2ЃЌ3ЃЉЕФЁА3ЪєХЩЩњЕуЁБP1ЕФзјБъЮЊЁЁ ЁЁЃЈжБНгЬюПеЃЉ
ЃЈ2ЃЉШєЕуPЕФЁА5ЪєХЩЩњЕуЁБP1ЕФзјБъЮЊЃЈ3ЃЌЉ9ЃЉЃЌдђЕуPзјБъЮЊЁЁ ЁЁЃЈжБНгЬюПеЃЉЃЛ
ЃЈ3ЃЉШєxжсе§АыжсЩЯвЛЕуPЃЈaЃЌ0ЃЉЕФЁАkЪєХЩЩњЕуЁБЮЊP1ЃЌЧвЯпЖЮPP1ЕФГЄЖШЮЊЯпЖЮOPГЄЖШЕФ2БЖЃЌдђkЃНЁЁ ЁЁЃЈжБНгЬюПеЃЉЃЛ
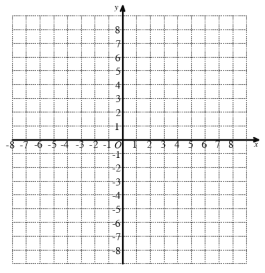
ЃЈ4ЃЉдкЃЈ3ЃЉЕФЬѕМўЯТЃЌШєЕуMдкyжсЩЯЃЌСЌНгMPЁЂMP1ЃЌЪЙMP1ЦНЗжЁЯPMOЃЌЧыжБНгаДГіЕуMЕФзнзјБъЃЈгУКЌaЕФДњЪ§ЪНБэЪОЃЉЃЎ
ЁОД№АИЁПЃЈ1ЃЉЃЈ7ЃЌЉ3ЃЉЃЛЃЈ2ЃЉЃЈЉ2ЃЌ1ЃЉЃЛЃЈ3ЃЉЁР2ЃЛЃЈ4ЃЉЕуMЕФзнзјБъЮЊЁР![]() aЃЎ
aЃЎ
ЁОНтЮіЁП
(1)ИљОнЬтвтЫуГіМДПЩ.
(2)ИљОнЬтвтСаГіЗНГЬзщЫуГіМДПЩ.
(3)ИљОнЬтвтСаГіЕШЪННтГіМДПЩ.
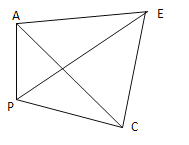
(4)ИљОнЬтвтЛГіЭМаЮ, Й§ЕуP1зїP1BЁЭMP,Й§ЕуMзїMCЁЭP1P,жЄУїЁїMCPЁеЁїP1PB,МДПЩЧѓГі.
НтЃК(1)P1(Љ2+3ЁС3,Љ2ЁС3+3),МДP1(7,Љ3)ЃЛ
ЙЪД№АИЮЊ(7,Љ3)ЃЛ
(2)ИљОнЬтвтЕУГіЗНГЬзщ:a+5b=3,5a+b=Ѓ9,НтЕУa=Ѓ2,b=1
ЙЪД№АИЮЊ(Љ2,1)ЃЛ
(3)P(a,0)ЕФЁАkЪєХЩЩњЕуЁБЮЊP1(a,ka),
ЁрPP1ЕФГЄЖШЮЊ|ka|,OPГЄЖШЮЊa,
ЁпЯпЖЮPP1ЕФГЄЖШЮЊЯпЖЮOPГЄЖШЕФ2БЖ,
Ёр|ka|ЃН2a,
ЁрkЃНЁР2,
ЙЪД№АИЮЊЁР2ЃЛ
(4)ЁпkЃНЁР2,
ЁрP1(a,ЁР2a),
ЕБP1(a,2a)ЪБ,
Й§ЕуP1зїP1BЁЭMP,Й§ЕуMзїMCЁЭP1P,
ЁпMP1ЦНЗжЁЯPMO,
ЁрAP1ЃНP1BЃНa,
ЁпMCЃНa,
ЁрЁїMCPЁеЁїP1PB(AAS),
ЁрMPЃНP1PЃН2a,
ЁрPCЃН![]() a,
a,
ЁрЕуMЕФзнзјБъЮЊЁР![]() aЃЎ
aЃЎ


ЁОЬтФПЁПдНРДдНЖрЕФШЫдкгУЮЂаХИЖПюЃЌАбЮЂаХеЫЛЇРяЕФЧЎзЊЕНвјааПЈНазіЬсЯжЃЌзд2016Фъ3дТ1ШеЦ№ЃЌУПИіЮЂаХеЫЛЇжеЩэЯэга1000дЊЕФУтЗбЬсЯжЖюЖШЃЌЕБРлМЦЬсЯжН№ЖюГЌЙ§1000дЊЪБЃЌГЌГіЕФВПЗжашжЇИЖ0.1ЃЅЕФЪжајЗбЃЌвдКѓУПДЮЬсЯжжЇИЖЕФЪжајЗбОљЮЊЬсЯжН№ЖюЕФ0.1ЃЅЃЎ
ЃЈ1ЃЉаЁгБ2018ФъПЊЪМЪЙгУЮЂаХЃЌЫћгУздМКЕФЮЂаХеЫЛЇЕквЛДЮЬсЯжН№ЖюЮЊ2000дЊЃЌашжЇИЖЪжајЗб дЊЃЛ
ЃЈ2ЃЉаЁССзд2016Фъ3дТ1КХжСНёЃЌгУздМКЕФЮЂаХеЫЛЇЙВЬсЯжШ§ДЮЃЌЬсЯжН№ЖюКЭЪжајЗбШчЯТЃЌ
ЕквЛДЮ | ЕкЖўДЮ | ЕкШ§ДЮ | |
ЬсЯжН№Жю/дЊ |
|
|
|
ЪжајЗб/дЊ | 0 | 0.2 | 3.0 |
ФЧУДаЁССЕФСНДЮЬсЯжЕФН№ЖюЗжБ№ЮЊЖрЩйдЊЃП