Question

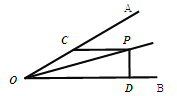
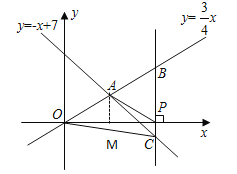
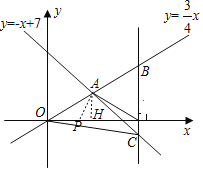
【题目】如图，在平面直角坐标系xOy中，已知正比例函数y＝x与一次函数y＝﹣x+7的图象交于点A，x轴上有一点P(a，0)．

（1）求点A的坐标；

（2）若△OAP为等腰三角形，则a＝　 　；

（3）过点P作x轴的垂线（垂线位于点A的右侧）、分别交y＝x和y＝﹣x+7的图象于点B、C，连接OC．若BC＝OA，求△OBC的面积．

Answer 1

【答案】（1）A(4，3)；（2）±5或8或；（3）28

【解析】

（1）点A是两直线的交点,其坐标即方程组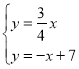的解；

（2）分OA＝PO、OA＝AP、AP＝OP适中情况，分别求解即可；

（3）P（a，0），则分别用含a的式子表示出B、C的坐标，从而表示出BC的长度，用勾股定理求得OA，然后根据BC＝OA求出a的值，从而利用三角形面积公式求解．

解：（1）由题意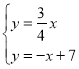：解得： ，

故点A（4，3）；

（2）点A（4，3），则OA＝，

①当OA＝PO=P1O时，

此时OA＝5＝PO=P1O，即a＝±5

②当OA＝AP时，如图，过点A做AM⊥x轴于点M

此时OM=MP=4

∴OP=8

则点P（8，0），即a＝8；

③当AP＝OP时，如图所示，连接AP，过点A作AH⊥x轴于点H，

AP＝PO＝a，则PH＝4﹣a，则（4﹣a）2+9＝a2，

解得：a＝；

综上，a＝±5或8或；

故答案为：±5或8或；

（3）∵P（a，0），则点B、C的坐标分别为：（a，a）、（a，﹣a+7），

∴BC=a-（-a+7）=a+a﹣7=

又∵BC＝OA且OA＝

∴＝×5＝7，

解得：a＝8，

故点P（8，0），即OP＝8；

△OBC的面积＝×BC×OP＝×7×8＝28．