题目内容
【题目】如图,在四边形ABCD中,∠A=60°, ∠ADC=∠ABC=90°,在AB、AD上分别找一点F、E,连接CE、EF、CF,当△CEF的周长最小时,则∠ECF的度数为______.

【答案】60°
【解析】
此题需分三步:第一步是作出△CEF的周长最小时E、F的位置(用对称即可);第二步是证明此时的△CEF的周长最小(利用两点之间线段最短);第三步是利用对称性求此时∠ECF的值.
分别作出C关于AD、AB的对称点分别为C1、C2,连接C1C2,分别交AD,AB于点E、F再连接CE、CF此时△CEF的周长最小,理由如下:
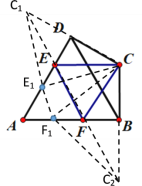
在AD、AB上任意取E1、F1两点
根据对称性:
∴CE=C1E,CE1=C1E1,CF=C2F,CF1=C2F1
∴△CEF的周长= CE+EF+CF= C1E+EF+C2F= C1C2
而△CE1F1的周长= CE1+E1F1+CF1= C1E1+E1F1+C2F1
根据两点之间线段最短,故C1E1+E1F1+C2F1>C1C2
∴△CEF的周长的最小为:C1C2.
∵∠A=60°, ∠ADC=∠ABC=90°
∴∠DCB=360°-∠A-∠ADC-∠ABC=120°
∴∠CC1C2+∠CC2C1=180°-∠DCB=60°
根据对称性:∠CC1C2=∠ECD,∠CC2C1=∠FCB
∴∠ECD+∠FCB=∠CC1C2+∠CC2C1=60°
∴∠ECF=∠DCB-(∠ECD+∠FCB)=60°
故答案为:60°

练习册系列答案
相关题目