Question

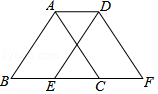
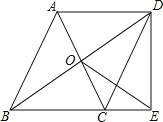
【题目】已知：如图，平行四边形ABCD的对角线相交于点O，点E在边BC的延长线上，且OE=OB，联结DE．

（1）求证：DE⊥BE；

（2）设CD与OE交于点F，若OF2+FD2=OE2，CE=3，DE=4，求线段CF的长．

Answer 1

【答案】（1）证明见解析（2）

【解析】（1）先根据平行四边形的性质，得出OD=OB，再根据OE=OB，得出OE=OB=OD，最后根据三角形内角和定理，求得∠OEB+∠OED=90°，即可得出结论．

（2）证明△OFD为直角三角形，得出∠OFD=90°．在Rt△CED中，由勾股定理求出CD=5．由三角形面积求出EF=．在Rt△CEF中，根据勾股定理求出CF即可．

（1）证明：∵平行四边形ABCD，∴OB=OD．∵OB=OE，∴OE=OD．

∴∠OED=∠ODE．∵OB=OE，∴∠OBE=∠OEB．

∵∠OBE+∠OEB+∠ODE+∠OED=180°，∴∠OEB+∠OED=90°．∴DE⊥BE；

（2）解：∵OE=OD，OF2+FD2=OE2，∴OF2+FD2=OD2．∴△OFD为直角三角形，且∠OFD=90°．

在Rt△CED中，∠CED=90°，CE=3，DE=4，∴CD2=CE2+DE2．

∴CD=5．又∵，∴．

在Rt△CEF中，∠CFE=90°，CE=3，，根据勾股定理得：．