题目内容
【题目】如图,完成下列推理,并填写理由,如图,∠B=∠D,∠1=∠2,求证:AB∥CD. 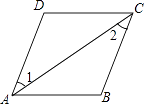
【证明】∵∠1=∠2(已知),
∴∥()
∴∠DAB+∠=180°()
∵∠B=∠D(已知)
∴∠DAB+∠=180°()
∴AB∥CD.
【答案】AD;BC;内错角相等两直线平行;B;两直线平行,同旁内角互补;D;等量代换
【解析】证明:∵∠1=∠2(已知), ∴AD∥BC(内错角相等,两直线平行),
∴∠DAB+∠B=180°(两直线平行,同旁内角互补),
∵∠B=∠D(已知),
∴∠DAB+∠D=180°(等量代换),
∴AB∥CD,
所以答案是:AD,BC,内错角相等两直线平行,B,两直线平行,同旁内角互补,D,等量代换.
【考点精析】根据题目的已知条件,利用平行线的判定与性质的相关知识可以得到问题的答案,需要掌握由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质.

练习册系列答案
相关题目
【题目】丽水苛公司将“丽水山耕”农副产品运往杭州市场进行销售.记汽车行驶时间为t小时,平均速度为v千米/小时(汽车行驶速度不超过100千米/小时).根据经验,v,t的一组对应值如下表:
v(千米/小时) | 75 | 80 | 85 | 90 | 95 |
t(小时) | 4.00 | 3.75 | 3.53 | 3.33 | 3.16 |
(1)根据表中的数据,求出平均速度v(千米/小时)关于行驶时间t(小时)的函数表达式;
(2)汽车上午7:30从丽水出发,能否在上午10:00之前到达杭州市?请说明理由:
(3)若汽车到达杭州市场的行驶时间t满足3.5≤t≤4,求平均速度v的取值范围.