Question

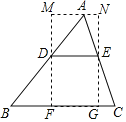
【题目】如图，在△ABC中，∠B=45°，AB=10，BC=8，DE是△ABC的中位线．过点D、E作DF∥EG，分别交BC于F、G，沿DF将△BDF剪下，并顺时针旋转180°与△AMD重叠，沿EG将△CEG剪下，并逆时针旋转180°与△ANE重叠，则四边形MFGN周长的最小值是__．

Answer 1

【答案】10+8．

【解析】

先判断出四边形MFGN是平行四边形，再判断出MN=FG=DE=4，进而判断出MF⊥BC时，四边形MFGN的周长最小，最后构造出直角三角形求出AH即可得出结论．

如图，

∵MN∥BC，FM∥GN，

∴四边形MFGN是平行四边形，

∴MF=NG，MN=FG，

∵DE是△ABC的中位线，

∴DE=BC=4，DE∥BC，

∴MN=FG=BC=4，

∴四边形MFGN周长=2（MF+FG）=2MF+8，

∴MF⊥BC时，MF最短，

即：四边形MFGN的周长最小，

过点A作AH⊥BC于H，

∴FM=AH

在Rt△ABH中，∠B=45°，AB=10，

∴AH=，

∴四边形MFGN的周长最小为2MF+8=10+8．

故答案为10+8．