题目内容
【题目】如图,我国海监船在钓鱼岛附近的O处观测到一可疑船正匀速直线航行我国海域,当该可疑船位于点O的北偏东30°方向上的点A处(OA=20![]() km)时,我方开始向对方喊话,但该可疑船仍匀速航行,40min后,又测得该可疑船位于点O的正北方向上的点B处,且OB=20km,求该可疑船航行的速度.
km)时,我方开始向对方喊话,但该可疑船仍匀速航行,40min后,又测得该可疑船位于点O的正北方向上的点B处,且OB=20km,求该可疑船航行的速度.

【答案】可疑船只的速度为30千米/小时.
【解析】
作AC⊥OB的延长线于点C,在直角三角形OAB中分别求得OC和AC,然后根据OB的值求得BC的值,利用勾股定理即可求得AB的距离,然后除以时间即可得到速度.
作AC⊥OB的延长线于点C,
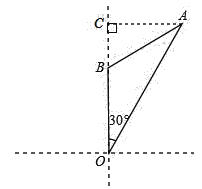
在Rt△OAB中,OA=20![]() ,∠O=30°,
,∠O=30°,
∴AC=![]() OA=10
OA=10![]() ,
,
OC=AOcos30°=20![]() ×
×![]() =30
=30
∵OB=20km,
∴BC=OC﹣OB=30﹣20=10千米,
由勾股定理得AB=![]() =20km,
=20km,
∴可疑船只的速度为20÷![]() =30千米/小时.
=30千米/小时.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目