题目内容
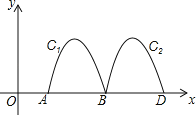
【题目】如图，二次函数y＝ax2﹣4ax（a≠0）的图象与直线y＝kx+3交于点A（﹣1，
）、点C两点．
（1）求a，k的值；
（2）点P在第一象限的抛物线上，其横坐标为t，连接PC、PA，设△PCA的面积为S，求S关于t的函数关系式：（直接写出t的取值范围）
（3）在（2）的条件下，作CE⊥x轴于E，点P直线y＝kx+3下方时，连接OP、BC交于D，连接ED，当∠ODE＝90°时，求t和S的值．
【答案】（1）a＝
，k＝；(2)S＝
,（4＜t＜6）或
,( t＞6)； (3)解得t=5，S=
.
【解析】
(1)将A（－1，
）代入二次函数y=ax2-4ax（a≠0）与直线y=kx+3中，可得a，k的值;
(2)分P点再BC中，与BC右侧两种情况讨论计算可得答案；
（3）由∠ODE=90°，
=-1，可得方程D点坐标，计算可得t，s的值.
解：（1）将A（－1，）代入二次函数y=ax2-4ax（a≠0）与直线y=kx+3；
可得：a＝，k＝；
（2）易得B点坐标（4，0），联立二次函数y=
，与一次函数y=
，可得
C点坐标（6，6），
如图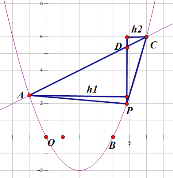
当P点再BC中间时候，横坐标为t，（4＜t＜6），可得P(t，
)，D(t，
)
=-()=
，
过点P做AC的垂线垂足为D，过A点做DP的垂线，设垂线长为
，过C点做DP的垂线, 垂线长为
,可得
=
=7,
= 
（）= 
（）7=,（4＜t＜6）；
如图，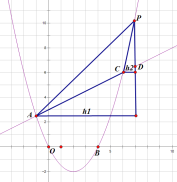
同理，当P点再C右侧时，即t＞6时，
同理过点PD⊥x轴，交AC与D点，过点C做垂线垂直PD，垂线长为，过A点做垂线垂直PD，垂线长为，易得
==7，=-()=
,
易得：= （）=,( t＞6)
（3）如图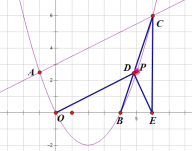
易得：E点坐标（6，0），B点（4，0），
可得BC直线的方程：y=3x-12，
设D点坐标为（x，3x-12），4＜x＜6，由∠ODE=90°，
可得=-1，可得，
，
化简得：
;
可得：
=3（舍去），
=
，
可得：D点坐标（，
）
可得OD的方程为y=
，
联立OD与二次函数的方程可得：
可得x=5，即t=5，
代入=,可得S=,
故答案：t=5，s=.
