Question

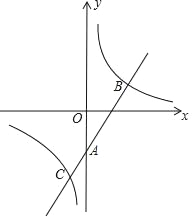
【题目】在平面直角坐标系中，抛物线y＝ax2﹣2ax﹣3与x轴交于A、B两点（点A在点B左侧），与y轴交于点C，顶点为D，且过点（2，﹣3a）．

（1）求抛物线的解析式；

（2）抛物线上是否存在一点P，过点P作PM⊥BD，垂足为点M，PM＝2DM？若存在，求点P的坐标；若不存在，说明理由．

（3）在（2）的条件下，求△PMD的面积．

Answer 1

【答案】（1）（1，﹣4）;（2）存在，（﹣，﹣）;（3）.

【解析】

（1）将点的坐标（2，﹣3a）代入抛物线表达式得：﹣3a＝4a﹣4a﹣3，即可求解；

（2）利用△PGM∽△MHD，得＝2，分别求出线段长度即可求解；

（3）利用S＝PMDM，即可求解．

（1）将点的坐标（2，﹣3a）代入抛物线表达式得：﹣3a＝4a﹣4a﹣3，解得：a＝1，

故抛物线的表达式为：y＝x2﹣2x﹣3，

令y＝0，解得：x＝3或﹣1，

即点A、B的坐标分别为（﹣1，0）、（3，0），

函数对称轴为x＝1，则点D的坐标为（1，﹣4）；

（2）存在．理由：

将点B、D的坐标代入一次函数表达式：y＝kx+b得：

，解得：，

即：直线BD的表达式为：y＝2x﹣6，

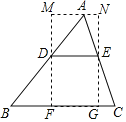
过点M作GH∥y轴，分别过点P、点D作x轴的平行线交于点G、H，

∵∠PMG+∠DMH＝90°，∠DMH+∠MDH＝90°，

∴∠PMG＝∠MDH，

∠PGM＝∠MHD＝90°，

∴△PGM∽△MHD，

∴＝2，

设点M、P的横坐标分别为m，n，则其坐标分别为（m，2m﹣6）、（n，n2﹣2n﹣3），

则：PG＝m﹣n，MH＝2m﹣6﹣（﹣4）＝2m﹣2，

即：m﹣n＝4m﹣4…①，

GM＝n2﹣2n﹣3﹣2m+6＝n2﹣2n﹣2m+3，DH＝m﹣1，

即：n2﹣2n﹣2m+3＝2m﹣2…②

①②联立并解得：n＝1或﹣（n＝1不合题意，舍去），

则n＝﹣，m＝，点M坐标为（，﹣），

故点P的坐标为（﹣，﹣）；

（3）由勾股定理得：

PM＝，

DM＝，

S＝PMDM＝．