题目内容
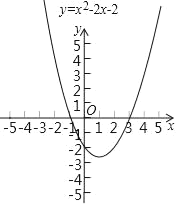
【题目】在实际问题中往往需要求得方程的近似解,这个时候,我们通常利用函数的图象来完成.如,求方程x2﹣2x﹣2=0的实数根的近似解,观察函数y=x2﹣2x﹣2的图象,发现,当自变量为2时,函数值小于0(点(2,﹣2)在x轴下方),当自变量为3时,函数值大于0(点(3,1)在x轴上方).因为抛物线y=x2﹣2x﹣2是一条连续不断的曲线,所以抛物线y=x2﹣2x﹣2在2<x<3这一段经过x轴,也就是说,当x取2、3之间的某个值时,函数值为0,即方程x2﹣2x﹣2=0在2、3之间有根.进一步,我们取2和3的平均数2.5,计算可知,对应的数值为﹣0.75,与自变量为3的函数值异号,所以这个根在2.5与3之间任意一个数作为近似解,该近似解与真实值的差都不会大于3﹣2.5=0.5.重复以上操作,随着操作次数增加,根的近似值越来越接近真实值.用以上方法求得方程x2﹣2x﹣2=0的小于0的解,并且使得所求的近似解与真实值的差不超过0.3,该近似解为_____
【答案】﹣0.75
【解析】
观察函数y=x22x2的图象,发现,当自变量为0时,函数值小于0,当自变量为1时,函数值大于0,求得1和0的平均数0.5,对应的数值为0.75,与自变量为1的函数值异号,再求1和0.5的平均数0.75,对应的数值为0.0625,即可求得这个根在0.75与0.5之间任意一个数作为近似解,由0.5(0.75)=0.25<0.3,即可求得近似值.
解:观察函数y=x2﹣2x﹣2的图象,发现,当自变量为0时,函数值小于0,当自变量为﹣1时,函数值大于0,因为抛物线y=x2﹣2x﹣2是一条连续不断的曲线,所以抛物线y=x2﹣2x﹣2在﹣1<x<0这一段经过x轴,也就是说,当x取﹣1、0之间的某个值时,函数值为0,即方程x2﹣2x﹣2=0在﹣1、0之间有根.
我们取﹣1和0的平均数﹣0.5,计算可知,对应的数值为﹣0.75,与自变量为﹣1的函数值异号,所以这个根在﹣1与﹣0.5之间,取﹣1和﹣0.5的平均数﹣0.75,计算可知,对应的数值为0.0625,与自变量为﹣0.5的函数值异号,所以这个根在﹣0.75与﹣0.5之间任意一个数作为近似解,该近似解与真实值的差都不会大于﹣0.5﹣(﹣0.75)=0.25<0.3,该近似解为﹣0.75,
故答案为﹣0.75.

 科学实验活动册系列答案
科学实验活动册系列答案