题目内容
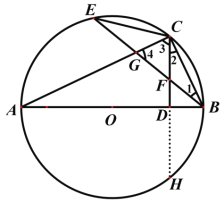
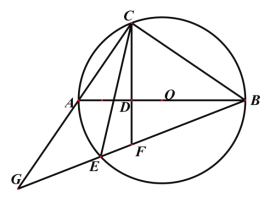
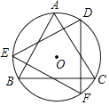
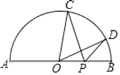
【题目】如图，在半圆⊙O中，直径AB=4，点C、D是半圆上两点，且∠BOC=84°，∠BOD=36°，P为直径上一点，则PC+PD的最小值为（ ）
A.4B.2
C.2
D.2
【答案】B
【解析】
作出点D关于AB的对称点E，连接CE交AB于点P，此时PC+PD最小，就等于CE的长，在△COE中求出CE长即可.
解：如图，在
O上作出点D关于AB的对称点E,连接CE，交AB于点P，
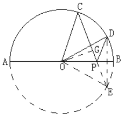
∴PC+PD=PC+PE=CE，CE为PC+PD的最小值 ，
连接OE、DE，过O作OG⊥CE于点G，
由垂径定理，得
，
∴∠DOB=∠EOB=36°，
∵∠BOC=84°，
∴∠COE=120°，
∵OC=OE，
∴∠E=∠OCE=30°，
∴OG=
OE=1，
∴由勾股定理得GE=
，
∴CE=
.
即PC+PD的最小值为.
故选B
练习册系列答案
优质课堂快乐成长系列答案
相关题目
【题目】某专卖店准备购进甲、乙两种运动鞋，其进价和售价如下表所示。已知用3000元购进甲种运动鞋的数量与用2400元购进乙种运动鞋的数量相同.
运动鞋价格 | 甲 | 乙 |
进价元/双) | m | m-30 |
售价(元/双) | 300 | 200 |
(1)求m的值；
(2)要使购进的甲，乙两种运动鞋共200双的总利润不少于21700元且不超过22300元，问该专卖店有几种进货方案?
(3)在(2)的条件下，专卖店决定对甲种运动鞋每双优惠a(60<a<80)元出售，乙种运动鞋价格不变，那么该专卖店要获得最大利润应如何进货?
