��Ŀ����
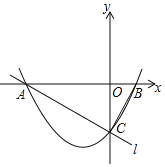
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪������y=![]() x2+
x2+![]() x��2��x�ύ��A��B���㣨��A�ڵ�B����ࣩ����y�ύ�ڵ�C��ֱ��l����A��C���㣬����BC��
x��2��x�ύ��A��B���㣨��A�ڵ�B����ࣩ����y�ύ�ڵ�C��ֱ��l����A��C���㣬����BC��
��1����ֱ��l�Ľ���ʽ��
��2����ֱ��x=m��m��0������������ڵ��������ڽ��ڵ�E����ֱ��l���ڵ�D������OD����OD��ACʱ�����߶�DE�ij���
��3��ȡ��G��0����1��������AG���ڵ�һ�����ڵ��������ϣ��Ƿ���ڵ�P��ʹ��BAP=��BCO����BAG�������ڣ������P�����ꣻ�������ڣ���˵�����ɣ�
���𰸡���1��y=![]() ����2��DE=
����2��DE=![]() ����3�����ڵ�P��
����3�����ڵ�P��![]() ��
��![]() ����ʹ��BAP=��BCO����BAG�����ɼ�����.
����ʹ��BAP=��BCO����BAG�����ɼ�����.
��������
��1��������Ŀ�еĺ�������ʽ������õ�A�͵�C�����꣬�Ӷ��������ֱ��l�ĺ�������ʽ��
��2�����������������ʵĸ����ߣ��������������ƺ��ɶ������Խ���⣻
��3���������⻭����Ӧ��ͼ�Σ�Ȼ�����������Ǻ���������á�OAC=��OCB��Ȼ�������Ŀ�е�������ͼ�Σ�����������Ǻ������ɶ������ɽ���⣮
��1����������y=![]() x2+
x2+![]() x-2��
x-2��
�൱y=0ʱ����x1=1��x2=-4����x=0ʱ��y=-2��
��������y=![]() x2+
x2+![]() x-2��x�ύ��A��B���㣨��A�ڵ�B����ࣩ����y�ύ�ڵ�C��
x-2��x�ύ��A��B���㣨��A�ڵ�B����ࣩ����y�ύ�ڵ�C��
���A��������-4��0������B��1��0������C��0��-2����
��ֱ��l����A��C���㣬��ֱ��l�ĺ�������ʽΪy=kx+b��
![]() ����
����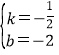 ��
��
��ֱ��l�ĺ�������ʽΪy=![]() x2��
x2��
��2��ֱ��ED��x�ύ�ڵ�F����ͼ1��ʾ��
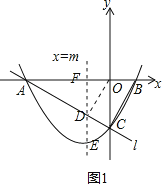
�ɣ�1���ɵã�
AO=4��OC=2����AOC=90�㣬
��AC=2![]() ��
��
��OD=![]() ��
��
��OD��AC��OA��OC����OAD=��CAO��
���AOD�ס�ACO��
��![]() ��
��
��![]() ����AD=
����AD=![]() ��
��
��EF��x�ᣬ��ADC=90�㣬
��EF��OC��
���ADF�ס�ACO��
��![]() ��
��
��ã�AF=![]() ��DF=
��DF=![]() ��
��
��OF=4-![]() =
=![]() ��
��
��m=-![]() ��
��
��m=-![]() ʱ��y=
ʱ��y=![]() ����
����![]() ��2+
��2+![]() ����-
����-![]() ��-2=-
��-2=-![]() ��
��
��EF=![]() ��
��
��DE=EF-FD=![]()
![]() ��
��![]() ��
��
��3�����ڵ�P��ʹ��BAP=��BCO-��BAG��
���ɣ���GM��AC�ڵ�M����PN��x���ڵ�N����ͼ2��ʾ��
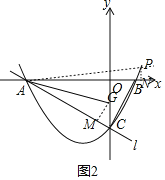
�ߵ�A��-4��0������B��1��0������C��0��-2����
��OA=4��OB=1��OC=2��
��tan��OAC=![]() ��tan��OCB=
��tan��OCB=![]() ��AC=2
��AC=2![]() ��
��
���OAC=��OCB��
�ߡ�BAP=��BCO-��BAG����GAM=��OAC-��BAG��
���BAP=��GAM��
�ߵ�G��0��-1����AC=2![]() ��OA=4��
��OA=4��
��OG=1��GC=1��
��AG=![]() ��
��![]() ����
����![]() ��
��
��ã�GM=![]() ��
��
��AM=![]() =
=![]() ��
��
��tan��GAM=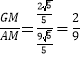 ��
��
��tan��PAN=![]() ��
��
���P��������n��![]() n2+
n2+![]() n-2����
n-2����
��AN=4+n��PN=![]() n2+
n2+![]() n-2��
n-2��
��![]() ��
��
��ã�n1=![]() ��n2=-4����ȥ����
��n2=-4����ȥ����
��n=![]() ʱ��
ʱ��![]() n2+
n2+![]() n-2=
n-2=![]() ��
��
���P��������![]() ��
��![]() ����
����
�����ڵ�P��![]() ��
��![]() ����ʹ��BAP=��BCO-��BAG��
����ʹ��BAP=��BCO-��BAG��