Question

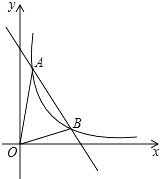
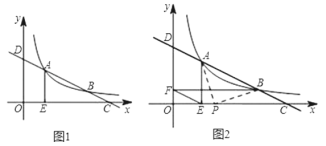
【题目】如图1，已知直线y=﹣x+m与反比例函数y=的图象在第一象限内交于A、B两点（点A在点B的左侧），分别与x、y轴交于点C、D，AE⊥x轴于E．

（1）若OECE=12，求k的值．

（2）如图2，作BF⊥y轴于F，求证：EF∥CD．

（3）在（1）（2）的条件下，EF=， AB=2，P是x轴正半轴上的一点，且△PAB是以P为直角顶点的等腰直角三角形，求P点的坐标．

Answer 1

【答案】（1）k=6；（2）详见解析；（3）P（3，0）．

【解析】

（1）分别设出一次函数解析式和反比例函数的解析式，代入点A的坐标，即可得出各解析式．

（2）连接AF、BE，过E、F分别作FM⊥AB，EN⊥AB，得出FM∥EN，再根据AE⊥x轴，BF⊥y轴，得出AE⊥BF，由此得出S△AEF=S△BEF，最后证出FM=EN，得出四边形EFMN是矩形，由此证出EF∥CD；

（3）由（2）得出EF=AD=BC和CD的值，再由直线解析式可得OD=m，OC=2m，得出OD=4，再根据EF∥CD，得出OF和0E、DF的值，最后根据EF=，AB=2得出EP的值，即可求出P点的坐标.

（1）设OE=a，则A（a，﹣a+m），

∵点A在反比例函数图象上，∴a（﹣a+m）=k，即k=﹣a2+am，

由一次函数解析式可得C（2m，0），

∴CE=2m﹣a，

∴OE．CE=a（2m﹣a）=﹣a2+2am=12，

∴k=（﹣a2+2am）=×12=6；

（2）连接AF、BE，过E、F分别作FM⊥AB，EN⊥AB，

∴FM∥EN，

∵AE⊥x轴，BF⊥y轴，

∴AE⊥BF，

S△AEF=AEOE=，

S△BEF=BFOF=，

∴S△AEF=S△BEF，

∴FM=EN，

∴四边形EFMN是矩形，

∴EF∥CD；

（3）由（2）可知，EF=AD=BC=，

∴CD=4，

由直线解析式可得OD=m，OC=2m，

∴OD=4，

又EF∥CD，

∴OE=2OF，

∴OF=1，0E=2，

∴DF=3，

∴AE=DF=3，

∵AB=2，

∴AP=，

∴EP=1，

∴P（3，0）．