Question

【题目】如图，在△ABC中，AB=AC=4，∠BAC=120°，M是BC的中点，点E是AB边上的动点，点F是线段BM上的动点，则ME+EF的最小值等于___.

Answer 1

【答案】3

【解析】

连接AM，作点M关于AB的对称点D，连接BD，DE，依据勾股定理，即可得到BD=BM=2，再根据当点D，E，F三点共线，且DF⊥BC时，EF+EM的最小值等于DF的长，利用勾股定理求得DF的长，即可得到ME+EF的最小值．

如图，连接AM，

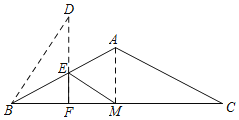
∵AB=AC=4，∠BAC=120°，M是BC的中点，
∴AM⊥BC，AM=AB=2，
∴Rt△ABM中，BM==2，
作点M关于AB的对称点D，连接BD，DE，则BD=BM=2，DE=ME，
当点D，E，F三点共线，且DF⊥BC时，EF+EM的最小值等于DF的长，
此时，Rt△BDF中，∠DBF=60°，∠D=30°，
∴BF=，
∴DF==3，
∴ME+EF的最小值等于3，
故答案为：3．