题目内容
【题目】如图，在矩形ABCD中，AB=10，BC=m，E为BC边上一点，沿AE翻折△ABE，点B落在点F处．
（1）连接CF，若CF//AE，求EC的长（用含m的代数式表示）；
（2）若EC=
，当点F落在矩形ABCD的边上时，求m的值；
（3）连接DF，在BC边上是否存在两个不同位置的点E，使得？若存
在，直接写出m的取值范围；若不存在，说明理由．
【答案】（1）EC=
；（2）
或
；（3）存在，
【解析】
（1）由翻折的性质可知BF⊥AE，CF//AE，所以
，根据直角三角形的性质，两锐角互余，可证得EF=EC，所以点E是BC的中点，即可求得EC的长；
（2）分两种情况进行分类讨论，当点F在AD边上，很容易可证得四边形ABEF是正方形，所以BE=
，就可求出m的值，当点F在CD上，由翻折的性质可得，
，AB=AF=10，在△ECF中由勾股定理可表示出CF的长，在△ADF中，由勾股定理即可求出m的值；
（3）由
可知，点F到AD边的距离为5,有两种情况，第一种情况当点F在矩形内，可得
，第二种情况当点F在AD边上方，可得
,要使在BC边上存在两个不同位置的点E，所以．
（1）连接CF，BF，BF交AE于点H，如下图所示：
∵△ABE沿AE翻折到了△AFE，由翻折可得：
∴BE=EF，BF⊥AE，
∴
，
∵CF//AE，
∴，
∴
，
，
∵BE=EF
∴∠BFE=∠FBE
∴∠EFC=∠ECF
∴EF=EC
∴EC=．
（2）①当点F在AD上，如下图所示：
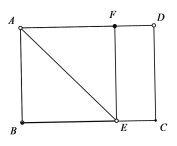
由翻折可得：
AB=AF=10，BE=EF，∠BAE=∠FAE=45
∵四边形ABCD是矩形，
∴∠ABE=90，AD//BC，
∴△ABE是等腰直角三角形，
∴AB=BE=AF=10，
∴四边形ABEF是正方形，
∵EC=
，
∴
=10
∴
；
②当点F在边CD上，如下图所示：
∵EC=，
∴
由翻折可得：
BE=EF，AB=AF=10，
在Rt△ECF中，由勾股定理得：
∴
，
在Rt△ADF中，由勾股定理得：
，
解得：
∴综上所述：或．
（3）存在，
过F点作AD的垂线，交AD于G点，设FG为h，
∵，
∴
，
∴
，
∴
，
①当点F再AD的下方，点E和点C重合时，如图所示：
在△AGF中，由勾股定理得：
,
∴
,
在△EHF中，由勾股定理得：
，
，
当点F在AD的上方时，点E和点C重合，如图所示：
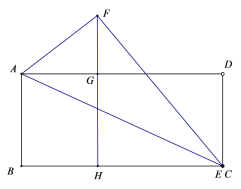
在△AGF中，由勾股定理得：
,
∴,
在△EHF中，由勾股定理得：
，
，
∴在BC边上存在两个不同位置的点E，，
故答案为：．
