题目内容
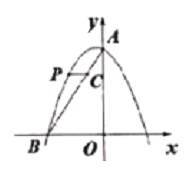
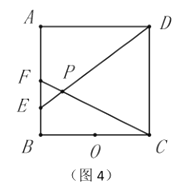
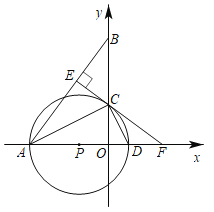
【题目】如图,△AOB中,A(-8,0),B(0,![]() ),AC平分∠OAB,交y轴于点C,点P是x轴上一点,⊙P经过点A、C,与x轴交于点D,过点C作CE⊥AB,垂足为E,EC的延长线交x轴于点F.
),AC平分∠OAB,交y轴于点C,点P是x轴上一点,⊙P经过点A、C,与x轴交于点D,过点C作CE⊥AB,垂足为E,EC的延长线交x轴于点F.
(1)求证:EF为⊙P的切线;
(2)求⊙P的半径.
【答案】(1)详见解析;(2)5
【解析】
(1)连接CP,根据等腰三角形的性质得到∠PAC=∠PCA,由角平分线的定义得到∠PAC=∠EAC,等量代换得到∠PCA=∠EAC,推出PC∥AE,于是得到结论;
(2)根据角平分线的定义得到∠BAC=∠OAC,根据等腰三角形的性质得到∠PCA=∠PAC,等量代换得到∠BAC=∠ACP,推出PC∥AB,根据相似三角形的性质即可得到结论.
(1)证明:连接CP, ∵AP=CP,
∴∠PAC=∠PCA,
∵AC平分∠OAB,
∴∠PAC=∠EAC,
∴∠PCA=∠EAC,
∴PC∥AE,
∵CE⊥AB,
∴CP⊥EF,
即EF是⊙P的切线;
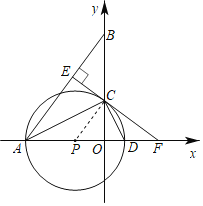
(2)由(1)知,PC∥AB,
∴△OPC∽△OAB,
∴ ![]()
∵A(-8,0),B(0,![]() ),
),
∴OA=8,OB=![]() ,
,
∴AB=![]()
![]() ,
,
∴ 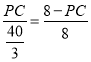 ,
,
∴PC=5,
∴⊙P的半径为5.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案
相关题目