题目内容
【题目】如图,将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ,将
,将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得
得![]() ,
,![]() 交
交![]() 于
于![]() 点.
点.
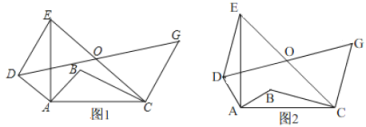
(1)求证:![]() ;
;
(2)若![]() ,
,![]() ,求
,求![]() 的长;
的长;
(3)若![]() ,
,![]() ,且
,且![]() 时,直接写出
时,直接写出![]() 的值.
的值.
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]() 或2.
或2.
【解析】
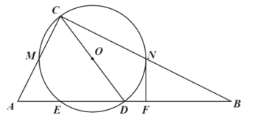
(1)延长![]() 交
交![]() 于点
于点![]() ,交
,交![]() 与点
与点![]() ,由旋转的性质可得
,由旋转的性质可得![]() ,旋转角
,旋转角![]() ,进一步证得DE∥CG,再根据旋转的性质得到说明
,进一步证得DE∥CG,再根据旋转的性质得到说明![]() ,证得四边形
,证得四边形![]() 为平行四边形,即可证明.
为平行四边形,即可证明.
(2) 连接![]() ,由题意得
,由题意得![]() 为等腰直角三角形,证得
为等腰直角三角形,证得![]() ;又因为
;又因为![]() ,即可
,即可![]() ,
,![]() ,
,![]() 三点共线;再证明四边形
三点共线;再证明四边形![]() 为矩形,得到
为矩形,得到![]() ,说明
,说明![]() 为等腰直角三角形,根据锐角的三角函数即可完成解答.
为等腰直角三角形,根据锐角的三角函数即可完成解答.
(3)先判断出四边形ABCF是矩形,进而得出△DFG是等腰直角三角形,即可得出![]() ,再用勾股定理得出
,再用勾股定理得出![]() ,再用
,再用![]() 建立等式即可得出结论.
建立等式即可得出结论.
(1)证明:延长![]() 交
交![]() 于点
于点![]() ,交
,交![]() 与点
与点![]() ,
,

由题意得:![]() ,旋转角
,旋转角![]() ,
,
∴在![]() 和
和![]() 中,
中,![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∵![]() 绕点
绕点![]() 旋转得到
旋转得到![]() ,
,![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得
得![]() ,
,
∴![]() ,
,
∴四边形![]() 为平行四边形,
为平行四边形,
∴![]() .
.
(2)连接![]() ,
,
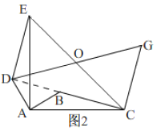
∵![]() ,
,![]() ,
,
∴![]() 为等腰直角三角形,
为等腰直角三角形,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,![]() ,
,![]() 三点共线,
三点共线,
又∵四边形![]() 为平行四边形,且
为平行四边形,且![]()
∴四边形![]() 为矩形
为矩形
∴![]() .
.
∵![]() 为等腰直角三角形
为等腰直角三角形
∴![]() ,
,
∴![]() .
.
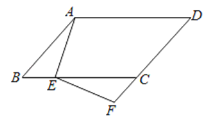
(3)如图3:延长DA,CG相交于点F
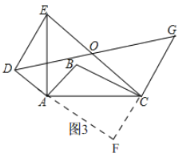
由旋转知,∠BAD=∠BCG=90°
∵∠BAF=∠BCF=90°
∴∠ABC=90°
∵四边形ABCF是矩形,
∴AF=BC,CF=AB,
∴FD=FG,
在Rt△DFG中,![]()
在RtACF中,AF2+CF2=AC2
∴AB2+ BC2=AC2
∴![]()
∴![]()
∴![]()
∴![]()
∴![]()
∴2AB2-5AB·BC+2BC2=0,
∴(2AB-BC)(AB-2BC)=0,
∴2AB-BC=0或AB-2BC=0,
∴![]() 或
或![]()
故答案为:![]() 或2
或2

练习册系列答案
相关题目