题目内容
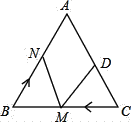
【题目】如图,在等边![]() 中,
中,![]() 厘米,
厘米,![]() 厘米.如果点
厘米.如果点![]() 以
以![]() 厘米/秒的速度运动,如果点
厘米/秒的速度运动,如果点![]() 在线段
在线段![]() 上由点
上由点![]() 向点
向点![]() 运动,点
运动,点![]() 在线段
在线段![]() 上由
上由![]() 点向
点向![]() 点运动.它们同时出发,若点
点运动.它们同时出发,若点![]() 的运动速度与点
的运动速度与点![]() 的运动速度相等.
的运动速度相等.
(1)经过![]() 秒后,
秒后,![]() 和
和![]() 是否全等?请说明理由.
是否全等?请说明理由.
(2)当两点的运动时间为多少时,![]() 是一个直角三角形?
是一个直角三角形?
【答案】(1)△BMN≌△CDM.理由见解析;
(2)当t=![]() 秒或t=
秒或t=![]() 秒时,△BMN是直角三角形.
秒时,△BMN是直角三角形.
【解析】
(1)根据题意得CM=BN=6cm,所以BM=4cm=CD.又∠B=∠C=60°,根据“SAS”可证明△BMN≌△CDM;
(2)设运动时间为t秒,分别表示出CM和BN.分①∠NMB=90°;②∠BNM=90°两种情况,运用直角三角形的性质求解.
解:(1)△BMN≌△CDM.理由如下:
∵VN=VM=3厘米/秒,且t=2秒,
∴CM=2×3=6(cm)
BN=2×3=6(cm)
BM=BC-CM=10-6=4(cm)
∴BN=CM
∵CD=4(cm)
∴BM=CD
∵∠B=∠C=60°,
∴△BMN≌△CDM.(SAS)
(2)设运动时间为t秒,△BMN是直角三角形.
有两种情况:
①当∠NMB=90°时,
∵∠B=60°,
∴∠BNM=90°-∠B=90°-60°=30°.
∴BN=2BM,
∴3t=2×(10-3t)
∴t=![]() (秒);
(秒);
②当∠BNM=90°时,
∵∠B=60°,
∴∠BMN=90°-∠B=90°-60°=30°.
∴BM=2BN,
∴10-3t=2×3t
∴t=![]() (秒)
(秒)
∴当t=![]() 秒或t=
秒或t=![]() 秒时,△BMN是直角三角形.
秒时,△BMN是直角三角形.

 中考解读考点精练系列答案
中考解读考点精练系列答案【题目】二次函数y=ax2+bx+c(a、b、c为常数且a≠0)中的x与y的部分对应值如下表:
x | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | 5 |
y | 12 | 5 | 0 | ﹣3 | ﹣4 | ﹣3 | 0 | 5 | 12 |
给出了结论:
(1)二次函数y=ax2+bx+c有最小值,最小值为﹣3;
(2)当﹣![]() <x<2时,y<0;
<x<2时,y<0;
(3)a﹣b+c=0;
(4)二次函数y=ax2+bx+c的图象与x轴有两个交点,且它们分别在y轴两侧
则其中正确结论的个数是( )
A. 1 B. 2 C. 3 D. 4




