Question

【题目】已知抛物线y=ax2+bx+3（a≠0）经过A（3，0）、B（4，1）两点，且与y轴交于点C．
（1）求抛物线的解析式；
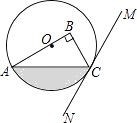
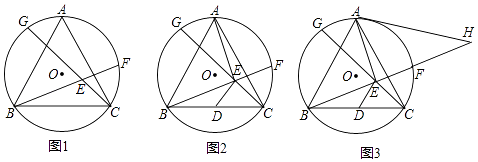
（2）如图（1），设抛物线与x轴的另一个交点为D，在抛物线的对称轴上找一点H，使△CDH的周长最小，求出H点的坐标并求出最小周长值．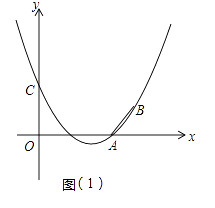

（3）如图（2），连接AC，E为线段AC上任意一点（不与A、C重合），经过A、E、O三点的圆交直线AB于点F，当△OEF的面积取得最小值时，求面积的最小值及E点坐标．

Answer 1

【答案】
（1）解：将点A（3，0），B（4，1）代入可得：

，

解得： ，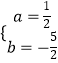

故函数解析式为y= x2﹣ x+3

（2）解：如图1中，连接DC、AC，AC交对称轴于H，连接DH，此时△CDH的周长最小．

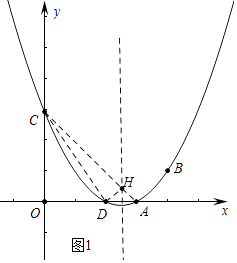
∵A、D关于对称轴对称，HD=HA，x

∴DH+CH=AC= =5，CD= = ，

∴△CDH的周长的最小值为5+ ，

∵A（3，0），C（3，0），

∴直线AC的解析式为y=﹣x+3，

∴H（ ， ）

（3）解：如图2中，作BD⊥OA于D．

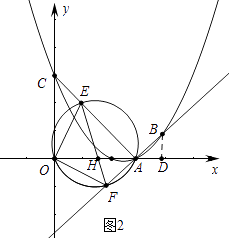
∵A（3，0），C（0，3），B（4，1），

∴OA=OC=3，AD=BD=1，

∴∠OAC=∠BAD=45°，

∵∠OAF=∠BAD=45°，

∴∠EAF=90°，

∴EF是△AEO的外接圆的直径，

∴∠EOF=90°，

∴∠EFO=∠EAO=45°，

∴△EOF是等腰直角三角形，

∴当OE最小时，△EOF的面积最小，

∵OE⊥AC时，OE最小，OC=OA，

∴CE=AE，OE= AC= ，

∴E（ ， ），S△EOF= = ．

∴当△OEF的面积取得最小值时，面积的最小值为 ，E点坐标（ ， ）

【解析】（1）把点A（3，0），B（4，1）的坐标代入抛物线解析式，利用待定系数法求二次函数解析式；（2）如图1中，连接DC、AC，AC交对称轴于H，连接DH，此时△CDH的周长最小．（3）如图2中，作BD⊥OA于D．首先证明△EOF是等腰直角三角形，当OE⊥AC时，△EOF的面积最小．