题目内容
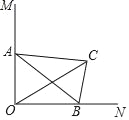
【题目】如图,在Rt△ABC中,BC=3,∠BAC=30°,斜边AB的两个端点分别在相互垂直的射线OM,ON上滑动.下列结论:①若C、O两点关于AB对称,则OA=3![]() ;②若AB平分CO,则AB⊥CO;③C,O两点间的最大距离是6;④斜边AB的中点D运动的路径长是
;②若AB平分CO,则AB⊥CO;③C,O两点间的最大距离是6;④斜边AB的中点D运动的路径长是![]() π,其中正确的有( )
π,其中正确的有( )
A. ①②B. ③④C. ②③④D. ①③④
【答案】D
【解析】
①先根据直角三角形30°的性质和勾股定理分别求AC和AB,由对称的性质可知:AB是OC的垂直平分线,所以OA=AC;
②如图2,当∠ABO=30°时,易证四边形OACB是矩形,此时AB与CO互相平分,但所夹锐角为60°,明显不垂直,或者根据四点共圆可知:A、C、B、O四点共圆,则AB为直径,由垂径定理相关推论:平分弦(不是直径)的直径垂直于这条弦,但当这条弦也是直径时,即OC是直径时,AB与OC互相平分,但AB与OC不一定垂直;
③当OC经过AB的中点E时,OC最大,则C、O两点距离的最大值为4;
④半径为2,圆心角为90°,根据弧长公式进行计算即可.
解:在Rt△ABC中,∵BC=3,∠BAC=30°,
∴AB=6,AC=![]() =3
=3![]() ,
,
①若C、O两点关于AB对称,
∴AB是OC的垂直平分线,
则OA=AC=3![]() ;
;
所以①正确;
②当∠ABO=30°时,∠OBC=∠AOB=∠ACB=90°,
∴四边形AOBC是矩形,
∴AB与OC互相平分,
但AB与OC的夹角为60°、120°,不垂直,
所以②不正确;
③取AB的中点为E,连接OE、CE,
∵∠AOB=∠ACB=90°,
∴OE=CE=![]() AB=3
AB=3
∵OC≤OE+EC,
∴当OC经过点E时,OC最大,
则C、O两点距离的最大值为6;
所以③正确;
④斜边AB的中点D运动路径是:以O为圆心,以3为半径的圆周的![]() ,
,
则:![]() ×2π3=
×2π3=![]() π,
π,
所以④正确;
综上所述,本题正确的有:①③④;
故选:D.


 阅读快车系列答案
阅读快车系列答案