题目内容
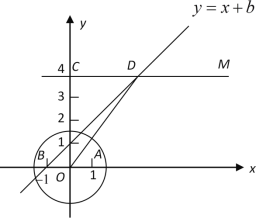
【题目】二次函数y＝ax2+bx+c的图象过A（2，0），B（0，﹣1）和C（4，5）三点．
（1）求二次函数的解析式；
（2）设二次函数的图象与x轴的另一个交点为D，求点D的坐标．
【答案】（1）y＝
x2﹣x﹣1；（2）D坐标为（﹣1，0）．
【解析】
（1）根据二次函数y=ax2+bx+c的图象过A，B和C三点，代入得出关于a，b，c的三元一次方程组，求得a，b，c，从而得出二次函数的解析式；
（2）令y=0，解一元二次方程，求得x的值，从而得出与x轴的另一个交点坐标
解：（1）把A（2，0），B（0，﹣1）和C（4，5）三点代入抛物线解析式y＝ax2+bx+c得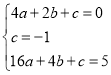
，
解得：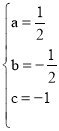
．
所以二次函数的解析式为y＝x2﹣x﹣1；
（2）当y＝0时，得 x2﹣x﹣1＝0；
解得x1＝2，x2＝﹣1，
∴点D坐标为（﹣1，0）．
【题目】某公司有
型产品
件，
型产品
件，分配给下属甲、乙两个商店销售，其中
件给甲店，
件给乙店，且都能卖完，两商店销售这两种产品每件的利润（元）如下表：
|
| |
甲店 |
|
|
乙店 |
|
|
（1）设分配给甲店型产品x件，则：
①分配给乙店的型产品_________件；
②分配给乙店的型产品_________件．
（2）这家公司卖出这
件产品的总利润为
（元），求关于
的函数关系式，并求出
的取值范围；
（3）若公司要求总利润不低于
元，说明有多少种不同分配方案，并将各种方案设计出来．
【题目】某初中学校欲向高一级学校推荐一名学生，根据规定的推荐程序：首先由本年级200名学生民主投票，每人只能推荐一人(不设弃权票)，选出了票数最多的甲、乙、丙三人.投票结果统计如图一：
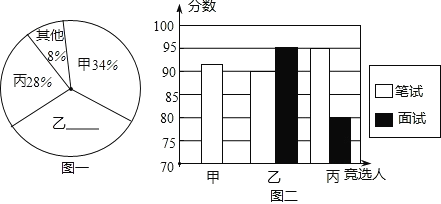
其次，对三名候选人进行了笔试和面试两项测试.各项成绩如下表所示：
测试项目 | 测试成绩/分 | ||
甲 | 乙 | 丙 | |
笔试 | 92 | 90 | 95 |
面试 | 85 | 95 | 80 |
图二是某同学根据上表绘制的一个不完全的条形图.
请你根据以上信息解答下列问题：
(1)补全图一和图二；
(2)请计算每名候选人的得票数；
(3)若每名候选人得一票记1分，投票、笔试、面试三项得分按照2:5:3的比确定，计算三名候选人的平均成绩，成绩高的将被录取，应该录取谁?
