题目内容
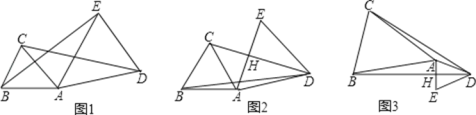
【题目】如图1,在![]() 中,
中,![]() 是直角,
是直角,![]() ,
,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的平分线,
的平分线,![]() 、
、![]() 相交于点
相交于点![]() .
.
(1)求出![]() 的度数;
的度数;
(2)判断![]() 与
与![]() 之间的数量关系并说明理由.(提示:在
之间的数量关系并说明理由.(提示:在![]() 上截取
上截取![]() ,连接
,连接![]() .)
.)
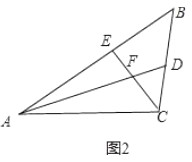
(3)如图2,在△![]() 中,如果
中,如果![]() 不是直角,而(1)中的其它条件不变,试判断线段
不是直角,而(1)中的其它条件不变,试判断线段![]() 、
、![]() 与
与![]() 之间的数量关系并说明理由.
之间的数量关系并说明理由.
【答案】(1)∠AFC=120°;(2)FE与FD之间的数量关系为:DF=EF.理由见解析;(3)AC=AE+CD.理由见解析.
【解析】
(1)根据三角形的内角和性质只要求出∠FAC,∠ACF即可解决问题;
(2)根据在图2的AC上截取CG=CD,证得△CFG≌△CFD(SAS),得出DF=GF;再根据ASA证明△AFG≌△AFE,得EF=FG,故得出EF=FD;
(3)根据(2)的证明方法,在图3的AC上截取AG=AE,证得△EAF≌△GAF(SAS)得出∠EFA=∠GFA;再根据ASA证明△FDC≌△FGC,得CD=CG即可解决问题.
(1)解:∵∠ACB=90°,∠B=60°,
∴∠BAC=90°﹣60°=30°,
∵AD、CE分别是∠BAC、∠BCA的平分线,
∴∠FAC=15°,∠FCA=45°,
∴∠AFC=180°﹣(∠FAC+∠ACF)=120°
(2)解:FE与FD之间的数量关系为:DF=EF.
理由:如图2,在AC上截取CG=CD,

∵CE是∠BCA的平分线,
∴∠DCF=∠GCF,
在△CFG和△CFD中,
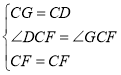 ,
,
∴△CFG≌△CFD(SAS),
∴DF=GF.∠CFD=∠CFG
由(1)∠AFC=120°得,
∴∠CFD=∠CFG=∠AFE=60°,
∴∠AFG=60°,
又∵∠AFE=∠CFD=60°,
∴∠AFE=∠AFG,
在△AFG和△AFE中,
 ,
,
∴△AFG≌△AFE(ASA),
∴EF=GF,
∴DF=EF;
(3)结论:AC=AE+CD.
理由:如图3,在AC上截取AG=AE,
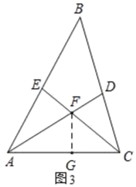
同(2)可得,△EAF≌△GAF(SAS),
∴∠EFA=∠GFA,AG=AE
∵∠BAC+∠BCA=180°-∠B=180°-60°=120°
∴∠AFC=180°﹣(∠FAC+∠FCA)=180°-![]() (∠BAC+∠BCA)=180°-
(∠BAC+∠BCA)=180°-![]() ×120°=120°,
×120°=120°,
∴∠EFA=∠GFA=180°﹣120°=60°=∠DFC,
∴∠CFG=∠CFD=60°,
同(2)可得,△FDC≌△FGC(ASA),
∴CD=CG,
∴AC=AG+CG=AE+CD.

 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案